Absolutt konvergens av alternerende rekke
Lagt inn: 05/12-2015 12:06
Hei igjen.
Jeg jobber med nr. 2:
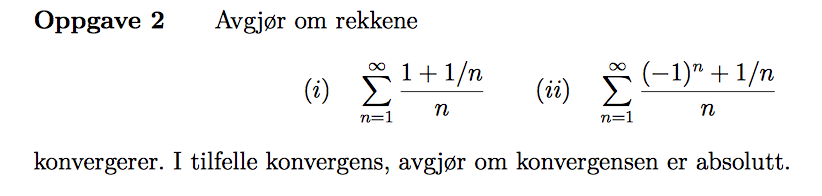
Jeg har funnet at rekken konvergerer, men når jeg skal finne ut om det er absolutt konvergens, har jeg noen spørsmål til fasiten, som sier dette..

Jeg skjønner HVA de har gjort, men jeg lurer på om det går an å gjøre det på en litt enklere måte.
Kan man kun bruke sammenligningstesten? Hvis jeg sammenligner absoluttverdien av den gitte rekken med den harmoniske rekken 1/n, vil jeg jo få at den gitte rekken divergerer. Jeg har lyst til å sette det opp slik:
[tex]abs(\frac{(-1)^n+\frac{1}{n})}{n}) > \frac{1}{n}[/tex]
Og siden 1/n er mindre OG divergerer, sier sammenligningstesten at den gitte rekken også divergerer, og dermed kan vi utelukke absolutt konvergens.
Er jeg helt på jordet eller funker dette?
Jeg jobber med nr. 2:
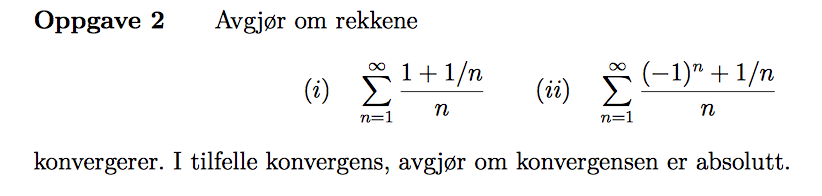
Jeg har funnet at rekken konvergerer, men når jeg skal finne ut om det er absolutt konvergens, har jeg noen spørsmål til fasiten, som sier dette..

Jeg skjønner HVA de har gjort, men jeg lurer på om det går an å gjøre det på en litt enklere måte.
Kan man kun bruke sammenligningstesten? Hvis jeg sammenligner absoluttverdien av den gitte rekken med den harmoniske rekken 1/n, vil jeg jo få at den gitte rekken divergerer. Jeg har lyst til å sette det opp slik:
[tex]abs(\frac{(-1)^n+\frac{1}{n})}{n}) > \frac{1}{n}[/tex]
Og siden 1/n er mindre OG divergerer, sier sammenligningstesten at den gitte rekken også divergerer, og dermed kan vi utelukke absolutt konvergens.
Er jeg helt på jordet eller funker dette?