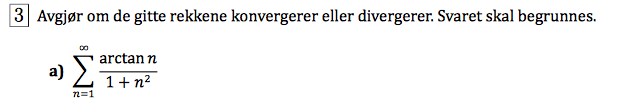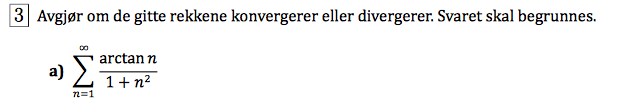matematikk.net

Hei igjen!

Jobber med innlevering 4 i matte 1 på NTNU, og har noen spørsmål angående oppgave 3..


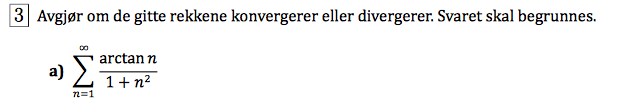
Jeg tenker at vi må bruke sammenligningstesten her, men jeg er ikke helt sikker på hvordan man går frem.
For å bruke testen må jeg altså velge en rekke som jeg vet konvergerer og som er større enn rekken jeg har. Jeg forstår ikke helt hvordan jeg bestemmer at den er større? Kan jeg bruke [tex]\frac{1}{n^2}[/tex] for å sammenligne?

Og hva skjer videre om jeg setter
[tex]\sum \frac{arctan(n)}{1+n^2} < \sum \frac{1}{n^2}[/tex] ?

Takk på forhånd!

Vi vet at $-\pi / 2 \leq \arctan x \leq \pi/ 2$ eller med andre ord $|\arctan x| \leq \pi/2$.

Du kan nok ikke gjøre den sammenligningen din uten å begrunne hvorfor den er lov. Målet ditt blir å sammenligne det med en større rekke du vet konvergerer. Hva får du om du bruker det ovenfor om $\arctan x$?

Har egentlig ikke peiling, men

[tex]\sum \frac{arctan(n)}{1+n^2} < \sum \frac{Pi}{2(1+n^2)}[/tex] ?

Haha, jeg tror jeg må ha inn dette med teskje..

Stemmer bra dette =) Herfra kan du enten bruke at $\frac{1}{1+n^2} < \frac{1}{n^2}$ (forstår du hvorfor?) eller bruke en eller annen sammenligningstest for å vise at integralet konvergerer =)

Nei, jeg forstår ikke det helt.. Jeg skjønner aldri hvor alt annet i uttrykket blir av. Hvor blir arctan(n) av på venstre side?
Fra [tex]\frac{Pi}{2(1+n^2)}[/tex] kan jeg vel sette Pi/2 utenfor summen, men hva skjer med 1-tallet?

Målet er jo bare å vise at uttrykket konvergerer ikke sant? Altså å vise at summen går mot noe endelig. For å gjøre dette brukes ofte sammenligningstesten. Vi sammenligner summen vår med en annen sum, som er større og kjent. Disse er ikke like på noen som helst måte, eneste vi må vite er at den ene er størst.

Som du sier vet vi når $\sum_{k=1}^\infty \frac{1}{k^p}$ konvergerer (p>). Med andre ord dersom rekken $a_n$ konvergerer og $| b_n |< |a_n|$ så må nødvendigvis $b_n$ også konvergerer. Absolutt konvergens medfører konvergens. Så

$
\sum \left| \frac{\arctan x} {1 + n^2} \right| \leq \sum \frac{ \pi / 2 } {1 + n^2}
$

Og siden høyre side konvergerer, må venstre side og konvergere siden den er mindre. Anbefaler deg for eksempel å lese seg mer opp på rekker. For eksempel gir påfølgende vide en ok innføring.

http://video.adm.ntnu.no/pres/501fbd4849ad1