Det stod ingen eksempel i Calculus boka, så jeg vet ikke hvordan jeg skal gjøre det.
1) En kurve er gitt ved y = (X^3) + X.
Finn sekanten til denne kurva gjennom punktene (-1, -2) og (2, 10).
Finn tangenten til kurva gjennom punktet (1, 2)
Noen som kan hjelpe meg? Helst ikke gi meg formler, de står i boka, jeg forstår bare ikke hva jeg kan gjøre, framgangsmåten.
Tusen takk!
Middelverdisetningen - hjelp
Moderatorer: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa
Hva er en sekant?Saxon skrev:Det stod ingen eksempel i Calculus boka, så jeg vet ikke hvordan jeg skal gjøre det.
1) En kurve er gitt ved y = (X^3) + X.
Finn sekanten til denne kurva gjennom punktene (-1, -2) og (2, 10).
Hva er en tangent, og hva trenger du for å beskrive den?Finn tangenten til kurva gjennom punktet (1, 2)
Sekantsetningen er det samme som middelverdisetningen i boka, så tipper jeg skal bruke den.
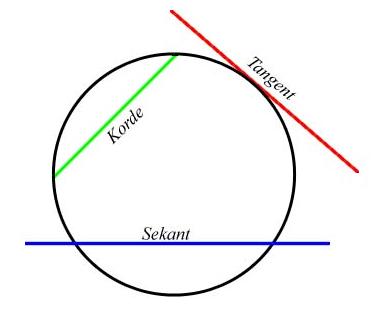
En sekant er en linje som går i gjennom en sirkel eller en kurve.
Tangent innen geometri er betegnelsen på en linje som berører en sirkel eller en annen kurve.
En sekant er en linje som går i gjennom en sirkel eller en kurve.
Tangent innen geometri er betegnelsen på en linje som berører en sirkel eller en annen kurve.
Vrøvl.Saxon skrev:Sekantsetningen er det samme som middelverdisetningen i boka, så tipper jeg skal bruke den.
En sekant er en linje som går i gjennom en sirkel eller en kurve.
En sekant er den unikt bestemte rette linja som går gjennom to utvalgte punkter på en kurve.
1. HAR du to punkter på kurven sekanten skal gå igjennom?
2. Gitt at du har det, hvordan finner du uttrykket for en rett linje ved hjelp av disse to punktene?
Vrøvl.Tangent innen geometri er betegnelsen på en linje som berører en sirkel eller en annen kurve.
Tangenten er den rette linja som, hvis den fins, er den beste lineære tilnærming til kurven i et gitt punkt.
Spesielt må tangentlinja gå igjennom dette punktet, samt at dets stigningstall er det samme som stigningstallet I det punktet på kurven.
-
meCarnival
- Riemann

- Innlegg: 1686
- Registrert: 07/09-2007 19:12
- Sted: Trondheim
(xˆ3 + x)' = 3xˆ2 + 1
Høgskolen i Sør-Trøndelag, Logistikkingeniør
Ingeniørmatematikk IV
Ingeniørmatematikk IV

