Bevis om injektiv funksjon

[Determined]

"La f : $[a,b] \rightarrow R$ være en kontinuerlig, injektiv funksjon. Vis at f er strengt monoton."

Jeg tenkte som følgende: vi har en kontinuerlig funksjon. Hvis vi kan vise at hvis den ikke er strengt monoton så er den ikke injektiv, så har vi funnet et bevis for setningen det gjelder. Det blir litt sånn om vi skal vise A => B, så kan vi vise dette ved å vise at "ikke B" => "ikke A". Men dette er opplagt, i og med at hvis den ikke er strengt monoton, så vil det det ikke til enhver $y \in V_f$ finnes bare én $x \in D_f$ slik at $y=f(x)$.

Men så lurte jeg litt på om det egentlig er så enkelt... surrer jeg?

[Pjolter]

Det er ikke helt riktig, men idéen er der! Du behøver kontinuiteten til [tex]f[/tex] for å nå helt frem. Husk hva definisjonen av en strengt monoton funksjon er. Hvis f ikke er kontinuerlig kan den godt ikke være strengt monoton, men fremdeles være injektiv. F. eks:

[tex]f = \begin{cases} \frac{1}{x} & x\neq 0 \\ 0 & x = 0 \end{cases}[/tex]

Det å vise at dersom [tex]f[/tex] er kontinuerlig så er det slik at om [tex]f[/tex] ikke er strengt monoton så er [tex]f[/tex] ikke injektiv er absolutt en god måte å gå frem på. Nå trenger du bare å få benyttet deg av kontinuiteten til [tex]f[/tex]. Bare å spørre hvis du sitter fast!

[Determined]

Hm. Holder det da å vise at for injektive funksjoner, så medfører ikke-monotoni diskontinuitet?

Anta da, isåfall, at f er kontinuerlig. Siden den er injektiv, har vi kun én $f(x)$ for hver x. Men siden den ikke er strengt monoton har vi $f(a)=f(b)$ for minste ett "sett" $a \neq b$. Dette er en selvmotsigelse.

Jeg har ikke lært noe om "bevisoppbygning", men hvis vi setter:
K: kontinuitet
I: injektivitet
M: streng monotoni
Så skal vi vise at K && I => M. Det første jeg gjorde var å vise at for K, så har vi "ikke M" => "ikke I". Deretter for I, så har vi "ikke M" => "ikke K".

Får håpe logikken min holder denne gangen!

[Pjolter]

Det blir dessverre ikke helt rett. Hvis du vil vise K [tex]\wedge[/tex] I [tex]\implies[/tex] M ved kontraposisjon må du vise at [tex]\lnot[/tex]M [tex]\implies \lnot[/tex](K [tex]\wedge[/tex] I) [tex]=[/tex] [tex]\lnot[/tex]K [tex]\lor[/tex] [tex]\lnot[/tex]M. Altså at hvis [tex]f[/tex] ikke er strengt monoton så er [tex]f[/tex] enten ikke kontinuerlig, ikke injektiv eller begge. Dette blir litt knotete.

Siden det virker som du er mer komfortabel med motsigelsesbevis kan vi prøve oss på den varianten. Da vil vi vise at dersom [tex]f[/tex] er kontinuerlig og injektiv så er det umulig at [tex]f[/tex] ikke er strengt monoton, m.a.o. [tex]f[/tex] kontinuerlig og injektiv medfører [tex]f[/tex] strengt monoton.

La nå [tex]f[/tex] være en kontinuerlig injektiv funksjon. Hvis du antar at [tex]f[/tex] ikke er strengt monoton kan du da finne en selvmotsigelse? (hint: Skjæringssetningen/Intermediate Value Theorem)

[Determined]

Hum. Hvis den ikke er strengt monoton, kan den likevel fortsatt være "svakt" monoton - blir det ikke vanskelig/umulig å utlede at dette er en selvmotsigelse for en kontinuerlig, injektiv funksjon?

(Lurer litt på om jeg skal dette: http://www.uio.no/studier/emner/matnat/ ... index.html emnet til høsten - lære litt om bevis generelt!)

[Gustav]

Hum. Hvis den ikke er strengt monoton, kan den likevel fortsatt være "svakt" monoton - blir det ikke vanskelig/umulig å utlede at dette er en selvmotsigelse for en kontinuerlig, injektiv funksjon?

(Lurer litt på om jeg skal dette: http://www.uio.no/studier/emner/matnat/ ... index.html emnet til høsten - lære litt om bevis generelt!)

Sikkert et bra fag dette. Lindstrøm som foreleser er garantert knallbra!

Hint til oppgaven: Anta at funksjonen ikke er strengt monoton. Da fins det tre punkter a<b<c slik at $f(a)\geq f(b)$ og $f(c)\geq f(b)$ (eller det motsatte). Bruk dette til å vise at funksjonen dermed ikke kan være injektiv (dersom den er kontinuerlig).

[Determined]

Hum. Hvis den ikke er strengt monoton, kan den likevel fortsatt være "svakt" monoton - blir det ikke vanskelig/umulig å utlede at dette er en selvmotsigelse for en kontinuerlig, injektiv funksjon?

(Lurer litt på om jeg skal dette: http://www.uio.no/studier/emner/matnat/ ... index.html emnet til høsten - lære litt om bevis generelt!)

Sikkert et bra fag dette. Lindstrøm som foreleser er garantert knallbra!

Hint til oppgaven: Anta at funksjonen ikke er strengt monoton. Da fins det tre punkter a<b<c slik at $f(a)\geq f(b)$ og $f(c)\geq f(b)$ (eller det motsatte). Bruk dette til å vise at funksjonen dermed ikke kan være injektiv.

Men det er nettopp det der jeg ikke skjønner. Betrakt følgende:



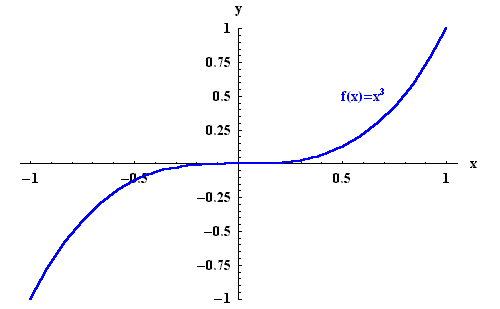
Den er kontinuerlig og ikke strengt monoton. Jeg syns det ser ut til at det for hver $y \in D_f$ finnes nøyaktig én $x \in D_f$ slik at $y=f(x)$...

[Gustav]

$f(x)=x^3$ er strengt monotont voksende. Kravet er at for alle x,y med x>y er f(x)>f(y). Den deriverte kan dog godt være 0 i et punkt

[Pjolter]

Det virker som du kanskje blander litt definisjoner. Kontinuitet er det vanskeligste, men den definisjonen trenger du ikke akkurat nå. Definisjonen av injektivitet er at [tex]f(x) = f(y) \implies x = y[/tex], i.e. [tex]f[/tex] sender ulike punkter på ulike punkter. Definisjonen av strengt monoton er vel at enten er det slik at [tex]x>y \implies f(x) > f(y)[/tex] (strengt voksende) eller [tex]x>y \implies f(x) < f(y)[/tex] (strengt avtagende). ([tex]\forall[/tex] [tex]x,y[/tex])

[Determined]

Hum. Jeg har visst surret fælt med begrepet om monotone funksjoner...

Hvis en funksjon ikke er strengt monoton, kan vi som plutarco sier finne a<b<c slik at $f(a) \geq f(b)$ og $f(b) \leq f(c)$ (om den er kontinuerlig!). Men dette strider mot injektiviteten siden vi da kan finne en y slik at det finnes flere x slik at $y=f(x)$.

Tror dette er korrekt... men fy søren jeg har surret nå!

[Gustav]

Hum. Jeg har visst surret fælt med begrepet om monotone funksjoner...

Hvis en funksjon ikke er strengt monoton, kan vi som plutarco sier finne a<b<c slik at $f(a) \geq f(b)$ og $f(b) \leq f(c)$ (om den er kontinuerlig!). Men dette strider mot injektiviteten siden vi da kan finne en y slik at det finnes flere x slik at $y=f(x)$.

Tror dette er korrekt... men fy søren jeg har surret nå!

Du burde kanskje formulere det litt mer presist, og henvise til intermediate value theorem som pjolter nevnte. Iallfall dersom svaret skal gis full score på en eksamen.

EDIT: Det du her egentlig bare gjør er å gjenfortelle definisjonen av injektivitet..

[Determined]

Siden vi har, under ikke-streng-monotoni, for $a<b<b$, at $f(a) \geq f(b)$ og $f(b) \leq f(c)$, od da har man ifølge middelverdisetningen vilkårlige $d$ og en $e$ slik at $f(a) \geq f(d) \geq f(b)$ og $f(b) \leq f(e) \leq f(c)$. Vi har der at $f(d)=f(e)$ for en eller annen $d$ og $e$. Vi har dermed, for $y=f(d)$ (eller $y=f(e)$), en $x_0 = d$ og en $x_1=e$. Dette strider mot at det for enhver $y$ bare skal finnes én $x$ slik at $y=f(x)$. Dette har da ledet til en selvmotisgelse, og følgelig må f være strengt monoton.



(Vanskeligste delen av matematikken, dette...)

[Pjolter]

Dette blir kanskje flisespikking, men middelverdisetningen/Sekantsetningen/Mean Value Theorem er ikke det man bruker her. Denne setningen omhandler den deriverte, og vi vet ikke om [tex]f[/tex] er deriverbar. Vi bruker skjæringssetningen/Intermediate Value Theorem som kort sagt sier at dersom [tex]f[/tex] er kontinuerlig på [tex][a,b][/tex] og [tex]s[/tex] er et tall (strengt) mellom [tex]f(a)[/tex] og [tex]f(b)[/tex] så finnes en [tex]c \in (a,b)[/tex] slik at [tex]f(c) = s.[/tex].

Jeg ser at det er dette du tenker på og ikke middelverdiesetningen, men jeg tenkte bare å få navnene riktig

Argumentet bør kanskje pusses litt på for å bli helt vanntett. Hvis noen av [tex]f(a),f(b),f(c)[/tex] er like er vi ferdig. Anta derfor at ingen av de er like, dvs. at [tex]f(a) > f(b)[/tex], [tex]f(c) > f(b)[/tex] og [tex]f(a) \neq f(c)[/tex]. La [tex]m = min(f(a),f(c))[/tex]. Da kan vi for enhver [tex]s \in (f(b),m)[/tex] finne [tex]c_1 \in (a,b)[/tex] og [tex]c_2 \in (b,c)[/tex] slik at [tex]f(c_1) = f(c_2) = s[/tex]. Men siden [tex]a<b<c[/tex] må vi ha at [tex]c_1 < c_2[/tex] og spesielt at [tex]c_1 \neq c_2[/tex]. Dette er en selvmotsigelse siden [tex]f[/tex] er injektiv. (Håper det er relativt åpenbart at [tex](f(b),m)[/tex] er ikke-tom.)

(Mulig dette kan gjøres mer raffinert, analyse har aldri vært min sterkeste side.)

[Determined]

Hum, jeg tror da jeg brukte middelverdisetningen... jeg bruker den jo to ganger?

Ditt svar er forøvrig bedre, så takk for det.