Driver litt gjettekonkurranse her nå, men tror det er dette de mener:
Vektorene [tex]\vec{u} = 2a+b[/tex], og [tex]\vec{v}=a-4b[/tex]
Finn den lineære kombinasjonen av [tex]2\vec{u} - 3\vec{v}[/tex].
[tex]\vec{u} = 2a+b => 2\vec{u} = 4a+2b[/tex]
[tex]\vec{v}=a-4b =>3\vec{v}=3a-12b[/tex]
_______________________________________________
[tex]\vec{w} = 2\vec{u} - 3\vec{v}[/tex]
[tex] \vec{w} =4a+2b - (3a-12b) [/tex]
[tex]\vec{w} =a + 14b[/tex]
_______________________________________________
Tolker dette dit at du får en vektor som går fra orego til punktet [tex](x,y)[/tex] [tex](1,14)[/tex]
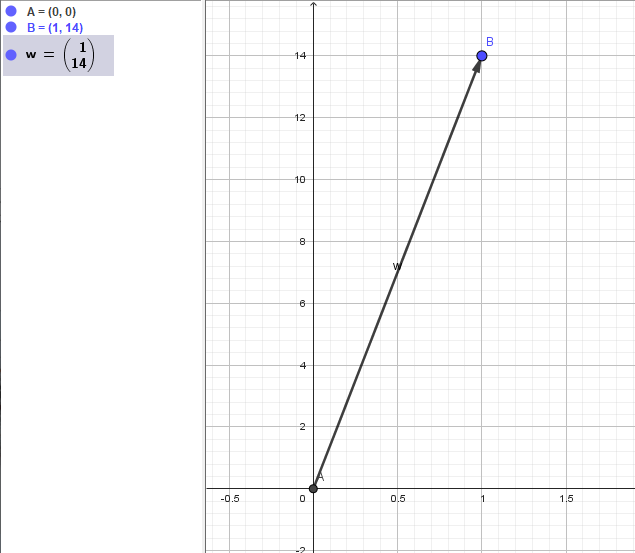
- Vektor A B.png (24.81 kiB) Vist 5803 ganger
Hvor svaret oppgaven ber etter er [tex]\vec{w} =a + 14b[/tex].
Mye mulig jeg tar feil, så greit å se om det er noen andre her som tolker dette annerledes
