Etter å ha sett litt på denne oppgaven og hva du har skrevet tolker jeg oppgaven slik:
Oppgave:
[tex]f(x) = 4e^x-e^{2^{x}}[/tex]
Oppgave 1.
Finn nullpunken(e)
Oppgave 2.
Finn funksjonens toppunkt ved regning.
__________________________________________________________
Oppgave 1.
Nullpunkten(e) er der hvor grafen krysser x-aksen.
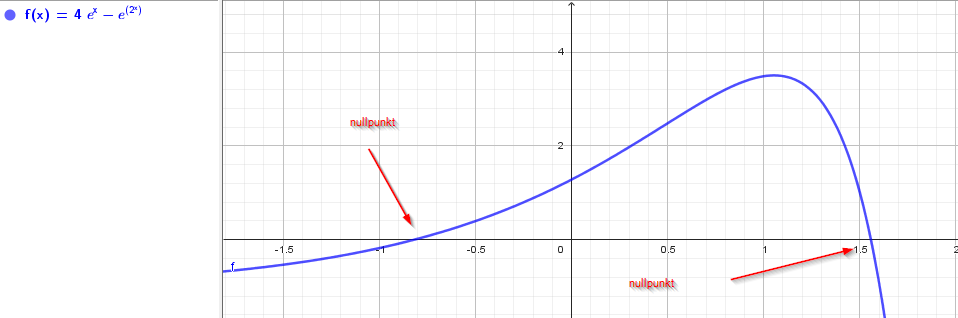
- nullpunkt.png (27.23 kiB) Vist 5774 ganger
Vi kan enten finne dette ved å sette funksjonen lik 0 og løse for x, altså:
[tex]4e^x-e^{2^{x}} = 0[/tex] Om dette skal løses for hånd må du bruke matte jeg tipper du ikke har vært borti før dersom dette er R1.
Så, vi bruker CAS til å løse dette for oss.
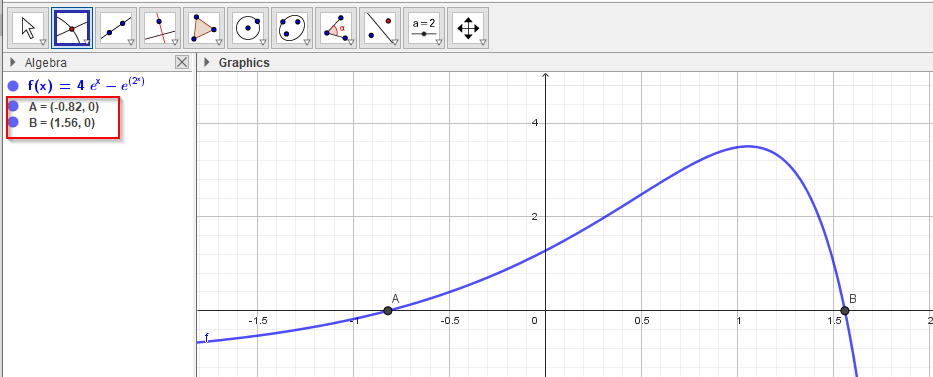
- Nullpunkt2.png (30.07 kiB) Vist 5774 ganger
Du har dermed nullpunkter i [tex] x=-0,82[/tex] og [tex]x = 1.56[/tex]
__________________________________________________________
Oppgave 2.
Finn funksjonens topppunkt ved regning.
Jeg anser det som urimelig å be deg finne dette ved regning, så antar at du enten har skrevet oppgaven feil fra starten av, eller at dette ikke er R1 pensum.
Dersom du skulle funnet toppunktet ved regning måtte du først derivert [tex]f(x) = 4e^x-e^{2^{x}}[/tex] og satt dette lik 0.
[tex]f'(x) = 4e^x-2^{x}*ln(2)*e^{2^{x}}[/tex]
[tex]4e^x-2^{x}*ln(2)*e^{2^{x}} = 0[/tex], Dersom dette er direkte løselig for hånd vet jeg ikke hvordan. Men mener å huske at du kan benytte newtons metode eller andre tilnærmins algoritmer for å estimere nullpunktene.
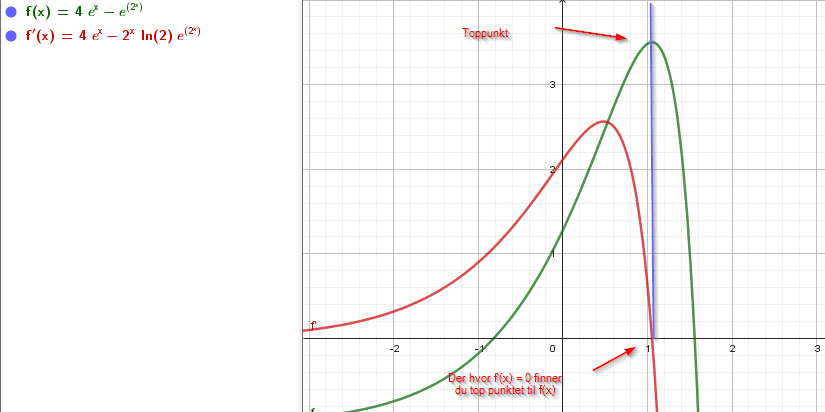
- Toppunkt.png (43.84 kiB) Vist 5774 ganger
Du kan altids finne topppunktet enkelt ved hjelp av CAS.
__________________________________________________________
Konklusjon...
Det er feil i oppgave/tekst, evt at dette ikke er en R1 matte?