Side 1 av 1
Kapitteltest 7 Oppgave 11
Lagt inn: 23/10-2022 13:04
av matteprat
Lurer på hvordan de går frem for å løse denne oppgaven. Kan skjønne en del av det og kommer frem til flere av svarene, men jeg bruker nok ikke riktige metoder, som gjerne gjør at det er litt flaks.

- tempImage7p4T9p.gif (2.15 MiB) Vist 2583 ganger
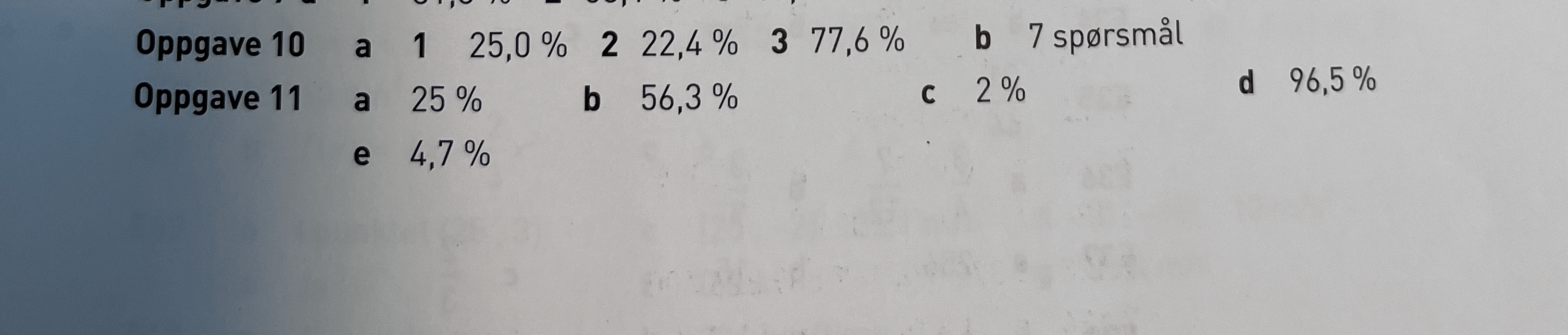
- tempImagexisITV.gif (810.55 kiB) Vist 2583 ganger
Re: Kapitteltest 7 Oppgave 11
Lagt inn: 23/10-2022 19:38
av SveinR
Lurer du like mye på alle oppgavene? Hva har du forsøkt selv?
Re: Kapitteltest 7 Oppgave 11
Lagt inn: 24/10-2022 10:04
av matteprat
Lurer i hovedsak på c,d og e. Men også hvordan man bør sette opp de ulike sannsynlighetene i a og b. Jeg forstår a og b da jeg mener det er ganske logisk, men lurer på om det er en bestemt måte man burde "angripe" oppgaven på, og sette det opp skikkelig.
I a forstår jeg at det er fire ulike muligheter hos et barn der begge foreldrene har aB. Da en unge kan få aa, aA, Aa og AA. Men jeg lurer på om man burde sette det opp på en bedre måte.
Re: Kapitteltest 7 Oppgave 11
Lagt inn: 24/10-2022 10:08
av matteprat
Og i b forstår jeg at sannsynligheten for at et barn ikke vil lide av sykdommen vil være (1-1/4) = 3/4.
Slik at sannsynligheten for at paret får to barn som ikke vil lide av sykdommen er (3/4)^2.
Men har ikke noe godt oppsett på det.
Re: Kapitteltest 7 Oppgave 11
Lagt inn: 24/10-2022 17:05
av LektorNilsen
I a) viser du jo tydelig at det er 25% sannsynlig ved å liste opp kombinasjonene, og det er gitt at alle kombinasjonene er like sannsynlige. Det er godt nok, så tar man gjerne med en svarsetning.
I b) bruker du at det må være 3/4 sannsynlig at ethvert barn av de to foreldrene IKKE rammes (følger av a) ). Vi ser da på hvert barn som et "delforsøk" og multipliserer sannsynlighetene, slik at det blir (3/4)^2 (som vi kan regne ut på kalkulator om vi vil ha en tilnærmet prosentverdi).
Slik jeg ser det, er det ikke behov for noe mer "oppsett" på disse deloppgavene, men er lurt med små forklaringer som leder leseren gjennom tankegangen.
Husk: Hovedpoenget er å løse oppgaven, altså besvare spørsmålene, og tankegangen må komme tydelig frem. Det er ikke et poeng i seg selv å skulle følge ett bestemt oppsett så lenge tankegangen er riktig ut fra situasjonen og tydelig formidlet.
Re: Kapitteltest 7 Oppgave 11
Lagt inn: 24/10-2022 17:25
av jos
Fornuftige råd!
Re: Kapitteltest 7 Oppgave 11
Lagt inn: 24/10-2022 23:50
av jos
NB! svaret under d) er rettet siden forrige innlegg
c)
Hvis sannsynligheten for at moren er bærer av sykdommen er 0.08, er sannsynligheten 0.08 * 0.5 for at hennes barn har genutgaven a fra henne. Sannsynligheten for genutgaven a fra faren er 0.5. Sannsynligheten for a fra begge er da 0.08 * 0.5 * 0.5 = 0.02, da hendelsene er uavhengige av hverandre. 0.02 er dermed sannsynligheten for at barnet vil lide av sykdommen.
d) Sannsynligheten for to friske barn i denne sammenhengen: $P(F\cap B) = P(F|B) * P(B) = 0.75^2\cdot 0.08 = 0.045$. Her er F hendelsen barna er begge friske og B er hendelsen mor er bærer av sykdommen.
e) Vi går ut fra at faren er bærer av sykdommen og at sjansene for at moren er bærer i utgangspunktet er 0.08. Vi bruker Bayes: La B være hendelsen mor er bærer av sykdommen og F hendelsen hennes to barn er friske.
$P(F|B) = 0.75^2= 0.5625, P(B) = 0.08, P(\overline B) = 0.92, P(F| \overline B) = 1$
Sannsynligheten for at mor er bærer når barna er friske:
$P(B|F) =\frac{P(F|B)\cdot P(B)}{P(F)} = \frac{P(F|B)\cdot P(B)}{P(F\cap B) + P(F \cap \overline B)} = \frac{P(F|B) \cdot
P(B)}{P(F|B)\cdot P(B) + P(F|\overline B)\cdot P(\overline B)} = $
$\frac{0.5625 \cdot 0.08}{0.5625 \cdot 0.08 + 1 \cdot 0.92} = 0.046$
Takk til mattebruker for påpekningen!