Side 1 av 1
Finne funksjon
Lagt inn: 04/10-2022 16:13
av eskils1111
Hei, sitter foreløpig fast med en oppgave ang det å finne en funksjon med ettpunktsformelen.
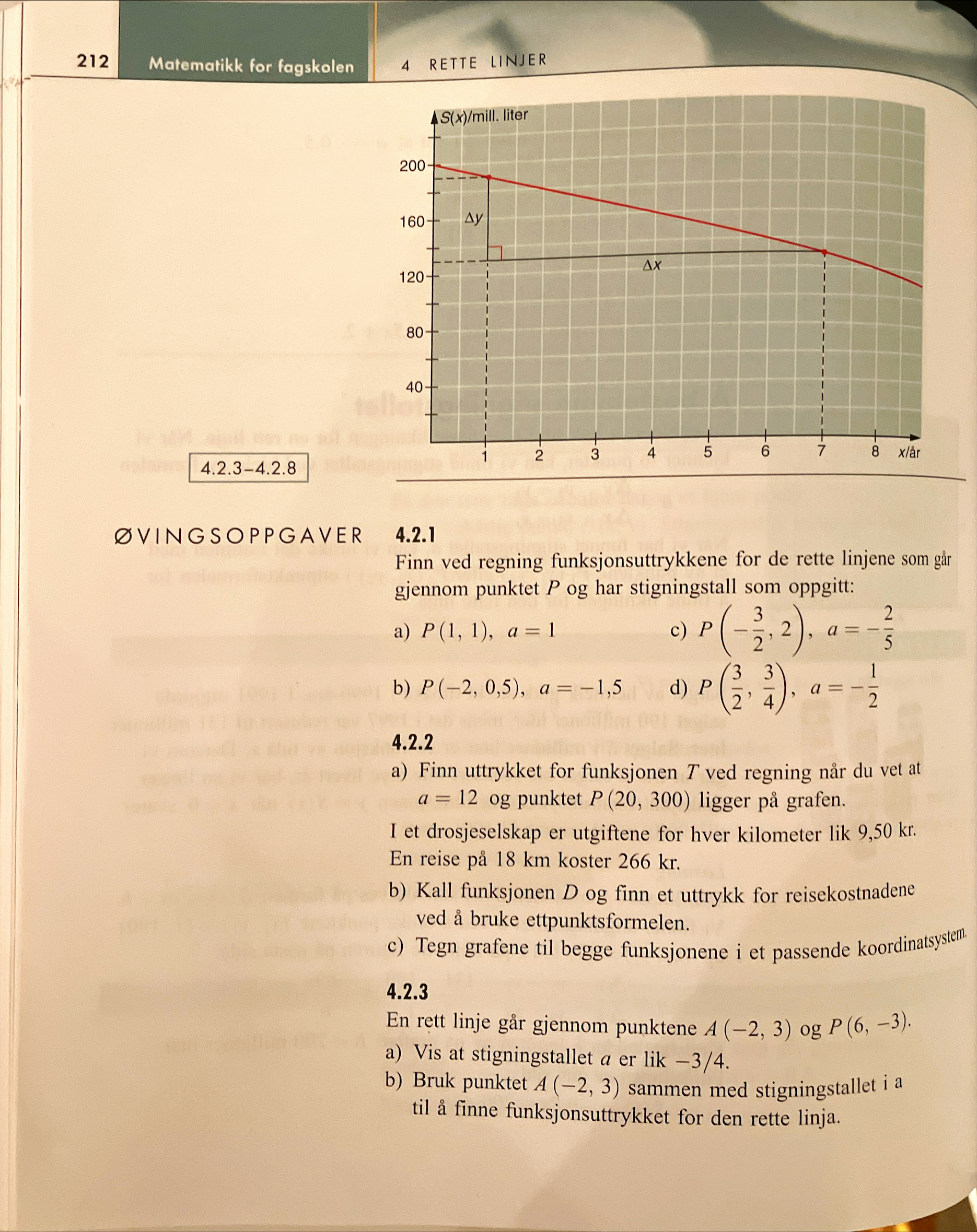
Selve det å finne funksjonen er vel forsåvidt greit, men i denne oppgaven så er Punkt 1 = (-(3/2), 2) a= -(2/5) (se vedlegg for bilde av oppgaven 4.2.1 C)
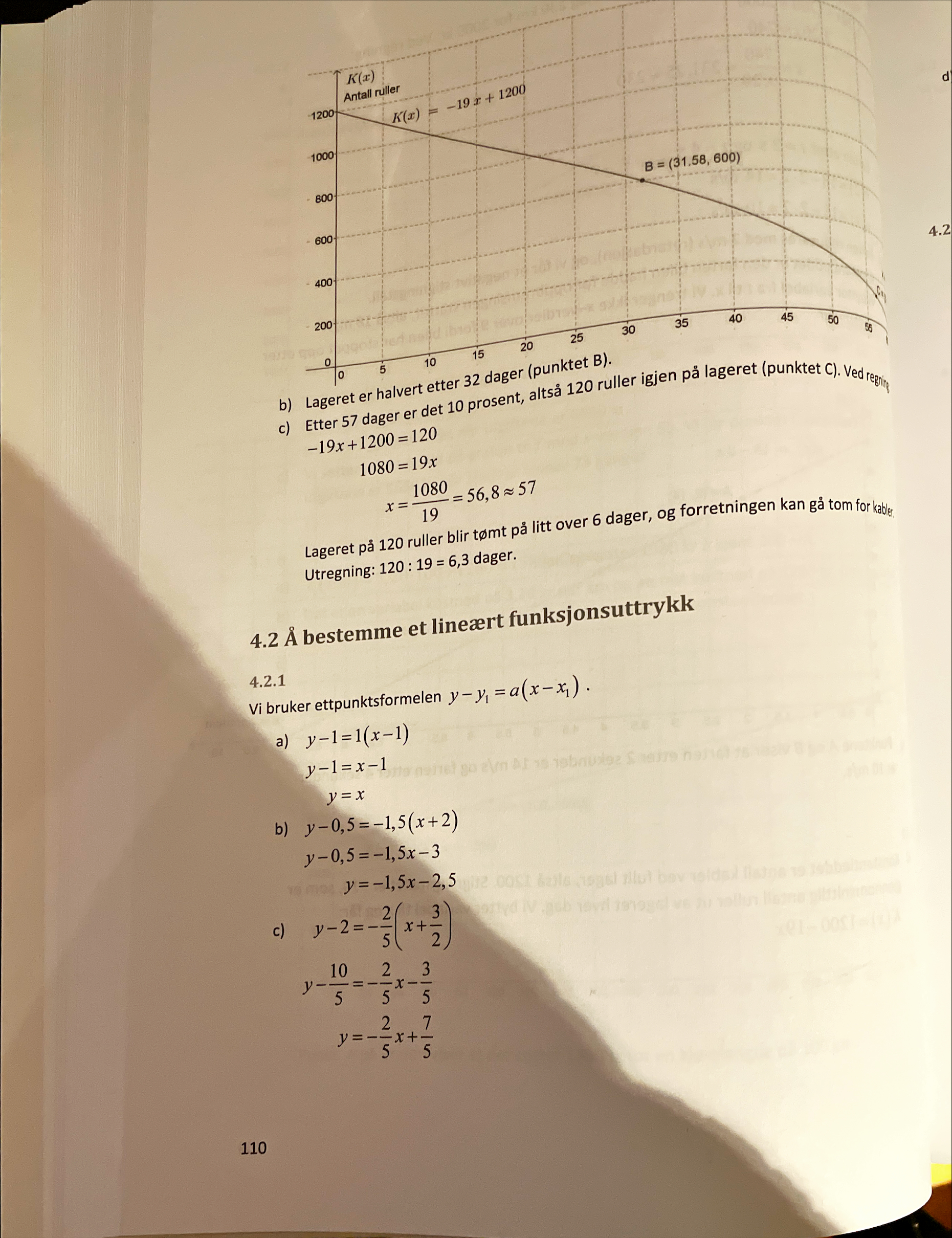
Skjønner ikke helt hvordan forfatteren utfører operasjonene i løsningsforslaget (se bilde Oppgave 4.2.1 Har noen mulighet for å forklare dette trinn for trinn? Takk for svar.
Dette gjelder oppgave 4.2.1 C) (Se vedlegg)
- Oppgave
- Oppgave matte.jpeg (4.1 MiB) Vist 2344 ganger
- Løsningsforslag
- Løsningsforslag 1.jpeg (3.56 MiB) Vist 2344 ganger
Re: Finne funksjon
Lagt inn: 04/10-2022 17:43
av SveinR
Ok, så vi har en rett linje som går gjennom $\biggl(-\frac{3}{2},2\biggr)$ og har stigningstall $a=-\frac{2}{5}$.
Løsningsforslaget ditt bruker da ettpunktsformelen, $y-y_1 = a(x-x_1)$, der $(x_1, y_1)$ er punktet vi har fått oppgitt.
Setter inn og får:
$y-2 = -\frac{2}{5}\biggl(x-\bigl(-\frac{3}{2}\bigr)\biggr)$
Som gir, ved bytte av fortegn når vi løser opp den ene parentesen:
$y-2 = -\frac{2}{5}\biggl(x+\frac{3}{2}\biggr)$
Ganger ut, og får:
$y-2 = -\frac{2}{5}\cdot x-\frac{2}{5}\cdot\frac{3}{2}$
Som gir:
$y-2 = -\frac{2}{5} x-\frac{6}{10}$
Hvor den siste brøken kan forkortes så vi får:
$y-2 = -\frac{2}{5} x-\frac{3}{5}$
Så gjør de om $2$ til en brøk med femdeler, så vi senere kan legge sammen brøkene:
$y-\frac{10}{5} = -\frac{2}{5} x-\frac{3}{5}$
Flytter over:
$y= -\frac{2}{5} x-\frac{3}{5}+\frac{10}{5}$
Legger sammen siste to leddene, og får til slutt:
$y= -\frac{2}{5} x+\frac{7}{5}$
Re: Finne funksjon
Lagt inn: 04/10-2022 17:46
av jos
Finne lineær funksjon når koordinatene til et punkt og stigningstallet er gitt.
La koordinatene til punktet være ($x_1, y_1$) og stigningstallet $a$.
Da har vi $ \frac{y - y_1}{x - x_1} = a$. For et fritt valgt punkt $(x,y)$, vil forholdet mellom differansen $y - y_1$ og differansen $x - x_1$ være konstant $ = a$. Ved innsetting av $(x,y) = (2,-\frac{3}{2}), \,$og $\, a = -\frac{2}{5}$ fås: $\frac{y -2}{x -(-\frac{3}{2})} = -\frac{2}{5}$. Vi kryssmultipliserer:
$(y - 2) * (-5) = 2 * ( x + \frac{3}{2}) => -5y + 10 = 2x + 3 => y = -\frac{2}{5}x + \frac{7}{5}$
Re: Finne funksjon
Lagt inn: 04/10-2022 18:27
av SveinR
Kan jo like gjerne vise enda en metode også, når vi først er igang - jeg personlig liker denne bedre enn ettpunktsformelen og andre varianter, siden det kun bruker funksjonsuttrykket (og dermed kan tilsvarende tankegang brukes i andre typer funksjonsuttrykk også):
En lineær funksjon er gitt på formen $y=ax+b$. Vi vet at $a = -\frac{2}{5}$, dermed har vi
$y=-\frac{2}{5}x+b$
For å bestemme konstantleddet $b$, kan vi bruke at vi vet at linjen går gjennom punktet $(x, y) = \biggl(-\frac{3}{2}, 2\biggr)$. Setter derfor inn dette i stedet for $x$ og $y$ i uttrykket, og får:
$2 = -\frac{2}{5}\cdot\biggl(-\frac{3}{2}\biggr) +b$
Som gir
$2 = \frac{3}{5}+b$
Løser for $b$, som gir
$b = 2 - \frac{3}{5} = \frac{10}{5}- \frac{3}{5} = \frac{7}{5}$
Og dermed har vi funnet uttrykket vårt:
$y=ax+b=-\frac{2}{5}x+ \frac{7}{5}$