Side 1 av 1
R1 - Derivasjon
Lagt inn: 18/03-2022 12:04
av Elisabeth123
Hei!
Jeg sliter med en oppgave og vet ikke helt hvilken formel/hvordan jeg skal løse den.
Noen som kan forklare meg hvordan de regner dette ut?
Oppgave 2.20 d)
Finn grenseverdiene:
lim x -->1 (2x^2-10x+8)/(2x-2)
Re: R1 - Derivasjon
Lagt inn: 18/03-2022 12:19
av Janhaa
Er jo strengt tatt grenseoppgave
Re: R1 - Derivasjon
Lagt inn: 18/03-2022 12:33
av Janhaa
Sjekk vedlegget mitt. Grenseoppgave med L’ Hopital’s rule gives -3
Håper dette stemmer.
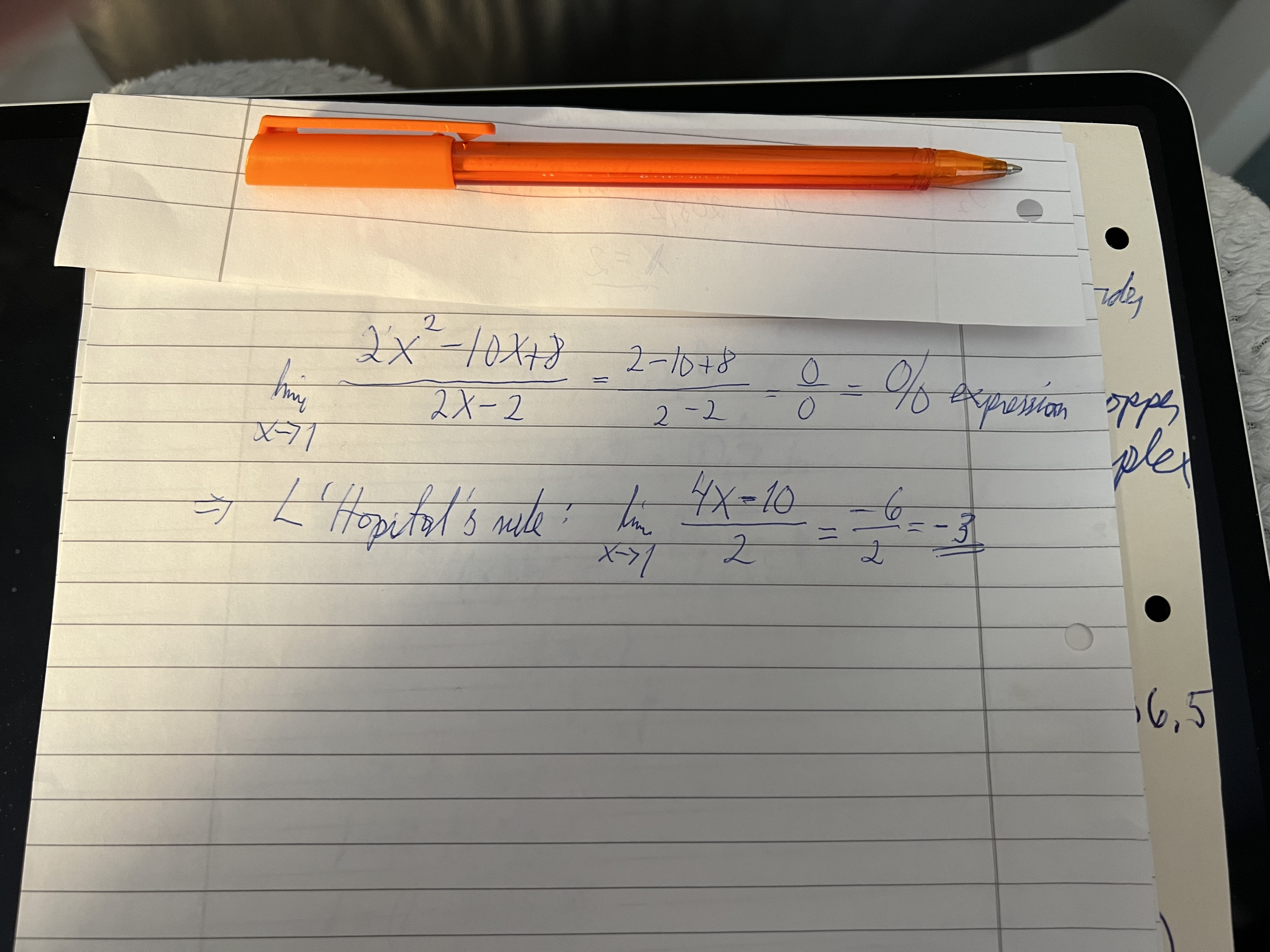
- EEEB2D74-7326-4DE3-8038-2C92B0BDB70E.jpeg (3.51 MiB) Vist 3656 ganger
Re: R1 - Derivasjon
Lagt inn: 18/03-2022 13:24
av LektorNilsen
Alternativ til L'Hôpital er å faktorisere teller og nevner og forkorte brøken

[tex]\frac{2x^{2}-10x+8}{2x-2}=\frac{2(x^{2}-5x+4)}{2(x-1)}=\frac{(x-4)(x-1)}{(x-1)}=x-4[/tex]
Setter vi nå inn 1 for x, får vi -3

Re: R1 - Derivasjon
Lagt inn: 18/03-2022 14:09
av Elisabeth123
LektorNilsen skrev: ↑18/03-2022 13:24
Alternativ til L'Hôpital er å faktorisere teller og nevner og forkorte brøken

[tex]\frac{2x^{2}-10x+8}{2x-2}=\frac{2(x^{2}-5x+4)}{2(x-1)}=\frac{(x-4)(x-1)}{(x-1)}=x-4[/tex]
Setter vi nå inn 1 for x, får vi -3

Hei og takk for svar! Men hvorfor forsvinner 2eren bare i nevneren? på siste utrekning så er den ikke med lengre, da står det kun: (x-1)
Re: R1 - Derivasjon
Lagt inn: 18/03-2022 15:18
av Janhaa
Elisabeth123 skrev: ↑18/03-2022 14:09
LektorNilsen skrev: ↑18/03-2022 13:24
Alternativ til L'Hôpital er å faktorisere teller og nevner og forkorte brøken

[tex]\frac{2x^{2}-10x+8}{2x-2}=\frac{2(x^{2}-5x+4)}{2(x-1)}=\frac{(x-4)(x-1)}{(x-1)}=x-4[/tex]
Setter vi nå inn 1 for x, får vi -3

Hei og takk for svar! Men hvorfor forsvinner 2eren bare i nevneren? på siste utrekning så er den ikke med lengre, da står det kun: (x-1)
Forkorter (x-1) med (x-1) , i teller og nevner
Re: R1 - Derivasjon
Lagt inn: 19/03-2022 13:27
av LektorNilsen
Elisabeth123 skrev: ↑18/03-2022 14:09
LektorNilsen skrev: ↑18/03-2022 13:24
Alternativ til L'Hôpital er å faktorisere teller og nevner og forkorte brøken

[tex]\frac{2x^{2}-10x+8}{2x-2}=\frac{2(x^{2}-5x+4)}{2(x-1)}=\frac{(x-4)(x-1)}{(x-1)}=x-4[/tex]
Setter vi nå inn 1 for x, får vi -3

Hei og takk for svar! Men hvorfor forsvinner 2eren bare i nevneren? på siste utrekning så er den ikke med lengre, da står det kun: (x-1)
Etter første steg, har vi 2 som felles faktor i teller og nevner. Da kan vi forkorte

Etter andre steget har vi (x-1) som felles faktor i teller og nevner, og kan forkorte igjen, slik at vi bare sitter igjen med x-4.
Re: R1 - Derivasjon
Lagt inn: 19/03-2022 14:18
av Elisabeth123
tusen takk for svar dere! Nå forstod jeg hva dere gjorde
