Umulig Kjegleoppgave

[Steviell]

Oppgave 8

En vanntank har form som en rett kjegle med
spissen nedover. Diameteren i toppflaten er
1,4 m, og høyden av tanken er 1,5 m.

a) Hvor mye rommer tanken? Oppgi svaret i liter.

b) Regn ut overflaten av tanken.

c)Hvor høyt står vannet i tanken hvis det er
500 liter vann i tanken?

A og B klarer jeg helt fint, men C er umulig. Meg og mattelæreren min får svaret 0.9, selv om fasiten sier 1.3 Kan noen si hva svaret er + nøyaktig hvordamn man regner der ut?

[Mattebruker]

Har prøvd å løyse problemet og får fasitsvaret ( 13 dm ).

Finn først radien( r ) i toppflata uttrykt ved den ukjende høgda( h ).

Hint: Samanlikne formlike trekantar.

[SpreVitenskapVidere]

Oppgave 8

En vanntank har form som en rett kjegle med
spissen nedover. Diameteren i toppflaten er
1,4 m, og høyden av tanken er 1,5 m.

a) Hvor mye rommer tanken? Oppgi svaret i liter.

b) Regn ut overflaten av tanken.

c)Hvor høyt står vannet i tanken hvis det er
500 liter vann i tanken?

A og B klarer jeg helt fint, men C er umulig. Meg og mattelæreren min får svaret 0.9, selv om fasiten sier 1.3 Kan noen si hva svaret er + nøyaktig hvordamn man regner der ut?

1.3 er faktisk riktig , skal komme med utfyllende svar snart men ideen er volumet er avhengig av både radius og høyde .

[SpreVitenskapVidere]

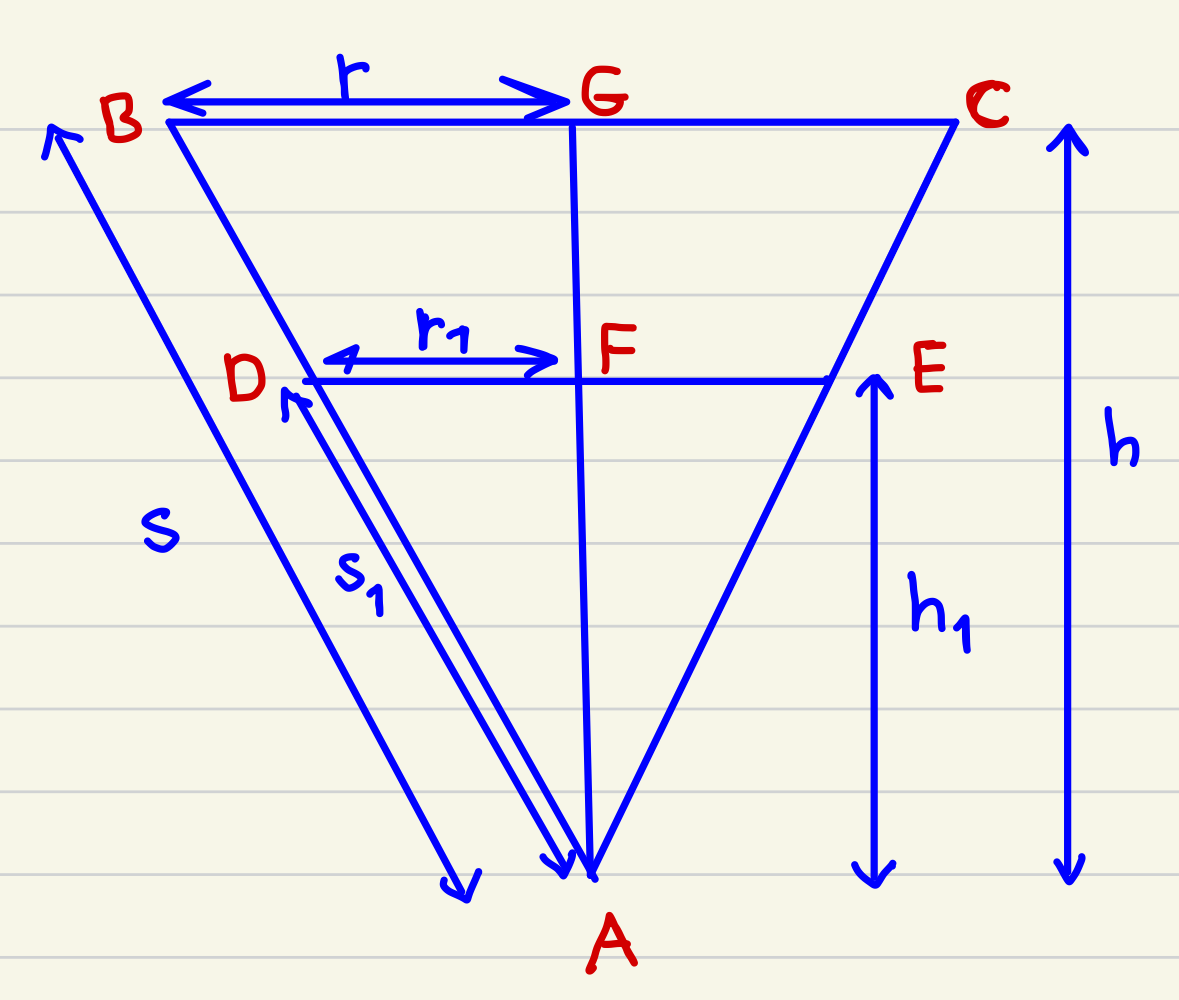
La $V$ være volumet av hele kjegle og $V_1$ volumet av kjeglen som er fylt med vann
\begin{align*}
V=\frac{1}{3}r^2\cdot h\\
V_1=\frac{1}{3}r_1^2\cdot h_1\\
\frac{V_1}{V}=\big(\frac{r_1}{r}\big)^{2}\cdot \frac{h_1}{h} \quad (1)
\end{align*}

KjegleMatteprat.png (93.82 kiB) Vist 1750 ganger

Fra figuren over ser vi at trekantene $\Delta ABG$ og $\Delta ADF$ er formlike og da er samsvarende lengder proporsjonale.
\begin{align*}
\frac{AF}{AG}&= \frac{AD}{AB}=\frac{DF}{BG}\\
\frac{h_1}{h}&= \frac{s_1}{s}=\frac{r_1}{r}\\
\frac{h_1}{h}&= \frac{r_1}{r}\quad \text{Sett dette i ligning (1)}\\
\frac{V_1}{V}&=\big(\frac{h_1}{h}\big)^{3}\\
\frac{0,5}{0,77}&=\big(\frac{h_1}{1,5}\big)^{3}\\
h_1&=(\frac{1,5^3\cdot 0,5}{0,77})^{\frac{1}{3}}=1,299
\end{align*}
Løsning via geogebra

KjegleMattepratGeogebra1.png (47.71 kiB) Vist 1750 ganger

KjegleMattepratGeogebra2.png (10.87 kiB) Vist 1750 ganger

[Steviell]

Har prøvd å løyse problemet og får fasitsvaret ( 13 dm ).

Finn først radien( r ) i toppflata uttrykt ved den ukjende høgda( h ).

Hint: Samanlikne formlike trekantar.

Tusen takk for utfyllende svar! Skal sette meg ned og prøve å forstå det. (P.S,- dette var en serdeles vanskelig oppgave til matematikk 2P å være. Ulikt noe annet jeg har vært borti i mattesammenheng. (Klarte alle oppgavene i kapittelet uten problemer, men så kom det her.) Spesielt!

Takk igjen.