Side 1 av 1
Matematikk 1T - 1.61 Aschehoug
Lagt inn: 10/08-2020 14:56
av FraPtilT
Bruk regnereglene for potenser til å avgjøre hvilket tall som er størst av [tex]\large 2^3^6 \:\: og \:\: 3^2^4[/tex]
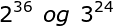
- CodeCogsEqn.gif (619 byte) Vist 2457 ganger
Forresten, når jeg har tosifrede tall i eksponenten i tex-koden så vises den ikke som den skal, er det noe triks?
Hvilke regler brukes for å regne så høye eksponenter? Det er vel ikke meningen at man skal gjøre dette for hånd?
Re: Matematikk 1T - 1.61 Aschehoug
Lagt inn: 10/08-2020 15:17
av Mattebruker
Hint:
2[tex]^{36}[/tex] = (2[tex]^{3}[/tex])[tex]^{12}[/tex]
(3[tex]^{24}[/tex]) = (3[tex]^{2}[/tex])[tex]^{12}[/tex]
Re: Matematikk 1T - 1.61 Aschehoug
Lagt inn: 10/08-2020 19:54
av Aleks855
FraPtilT skrev:
Forresten, når jeg har tosifrede tall i eksponenten i tex-koden så vises den ikke som den skal, er det noe triks?
Omring eksponenten med {krøllparentes}.
$2^{36}$
Se:
https://www.matematikk.net/matteprat/vi ... =4&t=34895
Re: Matematikk 1T - 1.61 Aschehoug
Lagt inn: 16/08-2020 12:21
av FraPtilT
Mattegjest skrev:Hint:
2[tex]^{36}[/tex] = (2[tex]^{3}[/tex])[tex]^{12}[/tex]
(3[tex]^{24}[/tex]) = (3[tex]^{2}[/tex])[tex]^{12}[/tex]
Takk, men for å avgjøre hvilket som er størst?
Re: Matematikk 1T - 1.61 Aschehoug
Lagt inn: 16/08-2020 12:40
av Gjest
[tex]8<9[/tex] dermed [tex]8^{12}<9^{12}[/tex]
Re: Matematikk 1T - 1.61 Aschehoug
Lagt inn: 29/08-2020 12:05
av FraPtilT
Gjest skrev:[tex]8<9[/tex] dermed [tex]8^{12}<9^{12}[/tex]
Oof, her var jeg sløv :p Takk anyway