matematikk.net

Er det noen som har fasit på eksamen?

Ikke før noen legger ut eksamensoppgavene

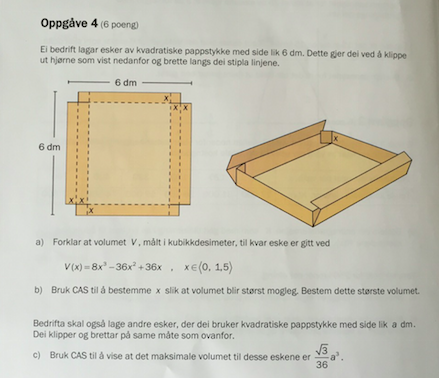
Mener jeg klarte resten av eksamen, men den j***a c-oppgava ødelagte alt...

Noen som kan vise hvordan man kommer frem til den?

http://gyazo.com/73f8b36c6291555929b1681975a33192

Lengden a er positiv så du kan se bort fra absoluttverdi tegnet.
Man burde egentlig også tegne fortegnskjema for den deriverte, men det er litt vanskelig i CAS...

noen som kan legge ut eksamen?

Sånn kan det f.eks. løses. Men de nullpunktene var jo ikke bare-bare, skjønner godt at denne var vrien.

Fint om noen kunne ha lagt ut oppgavesettet slik at noen får komt med et løsningsforslag jeg vet dessverre ikke hvordan jeg gjør det.

Hvor mange poeng regnes det at man må ha for å få en 6er etter den nye ordningen? Sjekka kjapt over nå og tror jeg får ca 30/34 på del 1 og 22/24 på del 2. Det blir til sammen 52/58, men vet ikke hvilken del som veies mest? Er vel lov å håpe

56*

Karakteren 6 viser at eleven har ”framifrå” kompetanse i faget. Når elever viser spesiell modenhet eller kunnskap i deler av besvarelsen, skal dette kunne veie opp for mindre feil og mangler i andre deler, slik at resultatet likevel kan bli en toppkarakter.

Er vel også del 1 som teller mest, siden den har 36 poeng, og del 2 har 24 poeng. Men til slutt så er poengsummen bare en pekepinn.

Fysikkmann97 skrev:56*

Karakteren 6 viser at eleven har ”framifrå” kompetanse i faget. Når elever viser spesiell modenhet eller kunnskap i deler av besvarelsen, skal dette kunne veie opp for mindre feil og mangler i andre deler, slik at resultatet likevel kan bli en toppkarakter.

Er vel også del 1 som teller mest, siden den har 36 poeng, og del 2 har 24 poeng. Men til slutt så er poengsummen bare en pekepinn.

56?

Ja, det er vel det som foreløpig er poengsummen du trenger for å få en sekser. Kan bli noe endret med forhåndssensuren.

4b
En fullgod besvarelse argumenterer for topp- og bunnpunkt.
Del 2
1
En fullgod besvarelse begrunner hvilke sannsynlighetsfordelinger som gjelder.
3a
Dersom graftegner på datamaskin ikke er brukt, gis maksimalt 1 poeng for hele deloppgave 3a.
4a
Kandidaten må argumentere for definisjonsmengden for å få full uttelling.
4b
Dersom CAS ikke er brukt, gis maksimalt 1 poeng for hele deloppgave 4b.
4c
Dersom CAS ikke er brukt, gis maksimalt 1 poeng for hele deloppgave 4c.

Fysikkmann97 skrev:Ja, det er vel det som foreløpig er poengsummen du trenger for å få en sekser. Kan bli noe endret med forhåndssensuren.

4b
En fullgod besvarelse argumenterer for topp- og bunnpunkt.
Del 2
1
En fullgod besvarelse begrunner hvilke sannsynlighetsfordelinger som gjelder.
3a
Dersom graftegner på datamaskin ikke er brukt, gis maksimalt 1 poeng for hele deloppgave 3a.
4a
Kandidaten må argumentere for definisjonsmengden for å få full uttelling.
4b
Dersom CAS ikke er brukt, gis maksimalt 1 poeng for hele deloppgave 4b.
4c
Dersom CAS ikke er brukt, gis maksimalt 1 poeng for hele deloppgave 4c.

Det var da veldig høyt :p blir ikke mange som får 6er da nei. En oppgave på del 1 og en på del 2 som nok har felt mange, 2 poeng på hver. Siste i begge

Siste på del 1 var da lett?

9^x - 3^x - 12 = 0
(3^2)^x - 3^x - 12 = 0
(3^x)^2 - 3^x - 12 = 0 Setter 3^x lik u og forutsetter at x > 0
u^2 - u -12 = 0 Bruker Vietes metode
(u -4)(u+3) = 0
u1 = 4 v u2 = - 3
Forkaster u2 siden å talogaritmen til ett negativt tall ikke går an (delvis løgn)

3^x = u1
3^x = 4
x lg 3 = lg 4
x = (lg 4)/(lg 3)

Fysikkmann97 skrev:Siste på del 1 var da lett?

9^x - 3^x - 12 = 0
(3^2)^x - 3^x - 12 = 0
(3^x)^2 - 3^x - 12 = 0 Setter 3^x lik u og forutsetter at x > 0
u^2 - u -12 = 0 Bruker Vietes metode
(u -4)(u+3) = 0
u1 = 4 v u2 = - 3
Forkaster u2 siden å talogaritmen til ett negativt tall ikke går an (delvis løgn)

3^x = u1
3^x = 4
x lg 3 = lg 4
x = (lg 4)/(lg 3)

Ser det nå ja. Brukte andregradsformel, bare gjorde ikke 3^x om til u, så fikk litt feil på a, b og c-verdiene. Tror ikke alle synes den var så lett, nei.

Hei! hvordan kan jeg laste opp eksamensoppgaven slik at noen får prøvd seg på et løsningsforslag?

Bruk "Last opp vedlegg"-knappen under der du skriver inn kommentarer.