Page 1 of 2
g(x)=x^2e^x
Posted: 03/02-2015 20:36
by MBSS
Jobber med denne funksjonen og skal finne topp, bunn og vendepunkter ved regning, sitter helt fast... noen som kan hjelpe?
Re: g(x)=x^2e^x
Posted: 03/02-2015 20:49
by pi-ra
MBSS wrote:Jobber med denne funksjonen og skal finne topp, bunn og vendepunkter ved regning, sitter helt fast... noen som kan hjelpe?
Litt usikker på hvordan funksjonen din ser ut. Er det sånn den skal se ut: [tex]x^{2} \cdot e^{x}[/tex]
Hva har du prøvd for å finne ekstremal- og vendepunktene?
Re: g(x)=x^2e^x
Posted: 03/02-2015 20:56
by pi-ra
Hint: For å finne topp-og bunnpunkt må du derivere [tex]g(x)[/tex], sette dette lik [tex]0[/tex] og sette opp et fortegnsskjema. For å finne vendepunkt må du gjøre det samme, men dobbeltderivere i stedet.
Re: g(x)=x^2e^x
Posted: 03/02-2015 21:23
by MBSS
pi-ra wrote:Hint: For å finne topp-og bunnpunkt må du derivere [tex]g(x)[/tex], sette dette lik [tex]0[/tex] og sette opp et fortegnsskjema. For å finne vendepunkt må du gjøre det samme, men dobbeltderivere i stedet.
Det har jeg skjønt, så kom meg til
g'(x)= 2x e^x
Men skjønner ikke helt hvordan jeg skal lage et fortegnsskjema til denne funksjonen...
Re: g(x)=x^2e^x
Posted: 03/02-2015 21:34
by pi-ra
Husk at det er et gangetegn mellom [tex]x^{2}[/tex] og [tex]e^{x}[/tex].
Det vil si du må bruke produktregelen når du deriverer:
[tex](uv)' = u'\cdot v + u\cdot v'[/tex]
Hva får du da?
Re: g(x)=x^2e^x
Posted: 03/02-2015 21:46
by MBSS
pi-ra wrote:MBSS wrote:Jobber med denne funksjonen og skal finne topp, bunn og vendepunkter ved regning, sitter helt fast... noen som kan hjelpe?
Litt usikker på hvordan funksjonen din ser ut. Er det sånn den skal se ut: [tex]x^{2} \cdot e^{x}[/tex]
Hva har du prøvd for å finne ekstremal- og vendepunktene?
Er sånn funksjonen ser ut ja. Får det til ved hjelp av kalkulator, men det er jo ikke det jeg skal.. Prøver å sette opp fortegnslinje, men får det ikke til..
Re: g(x)=x^2e^x
Posted: 03/02-2015 22:02
by pi-ra
[tex](uv)' = u'\cdot v + u\cdot v'[/tex]
[tex](x^{2}\cdot e^{x})'= 2x\cdot e^{x} + x^{2} \cdot e^{x} = e^{x}(x^{2}+2x)[/tex]
For å tegne opp et fortegnsskjema må du finne ut hvor du har nullpunkter for uttrykket utenfor parantesen og inni parantesen.
[tex]e^{x}[/tex]: Fortsetter å vokse og har derfor heller ingen nullpunkter.
[tex](x^{2}+2x)[/tex]: Ved ABC-formelen får vi at [tex]x_{1} = 0[/tex] og [tex]x_{2} = -2[/tex]
Det vil si det andre uttrykket kan skrives som [tex](x+0)(x+2)[/tex]
Når vi så tegner opp et fortegnsskjerma får vi:
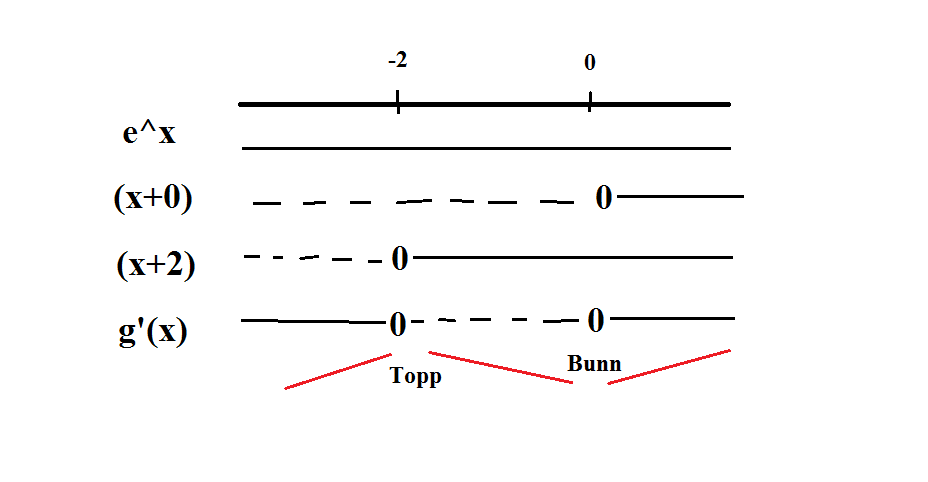
- fortegnskjemaaa.png (8.92 KiB) Viewed 8029 times
Re: g(x)=x^2e^x
Posted: 03/02-2015 22:05
by MBSS
pi-ra wrote:Husk at det er et gangetegn mellom [tex]x^{2}[/tex] og [tex]e^{x}[/tex].
Det vil si du må bruke produktregelen når du deriverer:
[tex](uv)' = u'\cdot v + u\cdot v'[/tex]
Hva får du da?
(2x+x^2)e^x?
Re: g(x)=x^2e^x
Posted: 03/02-2015 22:14
by MBSS
pi-ra wrote:[tex](uv)' = u'\cdot v + u\cdot v'[/tex]
[tex](x^{2}\cdot e^{x})'= 2x\cdot e^{x} + x^{2} \cdot e^{x} = e^{x}(x^{2}+2x)[/tex]
For å tegne opp et fortegnsskjema må du finne ut hvor du har nullpunkter for uttrykket utenfor parantesen og inni parantesen.
[tex]e^{x}[/tex]: Fortsetter å vokse og har derfor heller ingen nullpunkter.
[tex](x^{2}+2x)[/tex]: Ved ABC-formelen får vi at [tex]x_{1} = 0[/tex] og [tex]x_{2} = -2[/tex]
Det vil si det andre uttrykket kan skrives som [tex](x+0)(x+2)[/tex]
Når vi så tegner opp et fortegnsskjerma får vi:
fortegnskjemaaa.png
Tusen takk!
Da tror jeg at jeg skal klare resten av oppgaven! Var abc formelen som det skortet på mot slutten..
Re: g(x)=x^2e^x
Posted: 03/02-2015 22:20
by pi-ra
Så bra! Bare hyggelig.

Re: g(x)=x^2e^x
Posted: 04/02-2015 19:03
by MBSS
pi-ra wrote:Så bra! Bare hyggelig.

Stemmer det da at g''(x)= e^x(x^2+4x+2)
Re: g(x)=x^2e^x
Posted: 04/02-2015 19:09
by pi-ra
Jepp, det stemmer!
Re: g(x)=x^2e^x
Posted: 05/02-2015 19:05
by MBSS
pi-ra wrote:Jepp, det stemmer!
Fikk til vendepunktene, men så kom spørsmålet om: arealet som er avgrenset av den positive x aksen, grafen til G og linja x =1
Svaret jeg får samsvarer ikke med fasiten...
Jeg integrerer og får (1/3* x^3)e^x
Legger så inn x=1 i funksjonen og trekker fra funksjonen med x=0 og får da 1/3*e
I fasiten står det e-2
Hvor blir det feil?
Re: g(x)=x^2e^x
Posted: 05/02-2015 19:15
by pi-ra
Her har du integrert feil. Du må bruke delvis integrasjon siden du har [tex]x[/tex] i begge ledd. Hva får du da?
Re: g(x)=x^2e^x
Posted: 05/02-2015 21:30
by MBSS
pi-ra wrote:Her har du integrert feil. Du må bruke delvis integrasjon siden du har [tex]x[/tex] i begge ledd. Hva får du da?
(X^2-2x)e^x+C
Som gir -1*e?