1T eksamen våren 2017 med løsningsforslag
Moderatorer: Aleks855, Gustav, Nebuchadnezzar, Janhaa, DennisChristensen, Emilga
Det er lagt ut løsningsforslag på del 2, så du kan vel rette selv? Så er det bare å spørre hvis noe med løsningsforslaget er uklart?Spiderman98 skrev:Kan noen rette min del 2? Er ganske desperat etter 6eren, og føler at alt i del 2 jeg har gjort bør gi meg alt riktig. Kanskje noen 1 poeng feil for forklaringer. Hva tenker dere?
-
Gjest_1
Tror, jeg har sett på greia di. Ser ut som du får alt riktig på del 2.mattemarkus skrev:Det er lagt ut løsningsforslag på del 2, så du kan vel rette selv? Så er det bare å spørre hvis noe med løsningsforslaget er uklart?Spiderman98 skrev:Kan noen rette min del 2? Er ganske desperat etter 6eren, og føler at alt i del 2 jeg har gjort bør gi meg alt riktig. Kanskje noen 1 poeng feil for forklaringer. Hva tenker dere?
-
Gjest
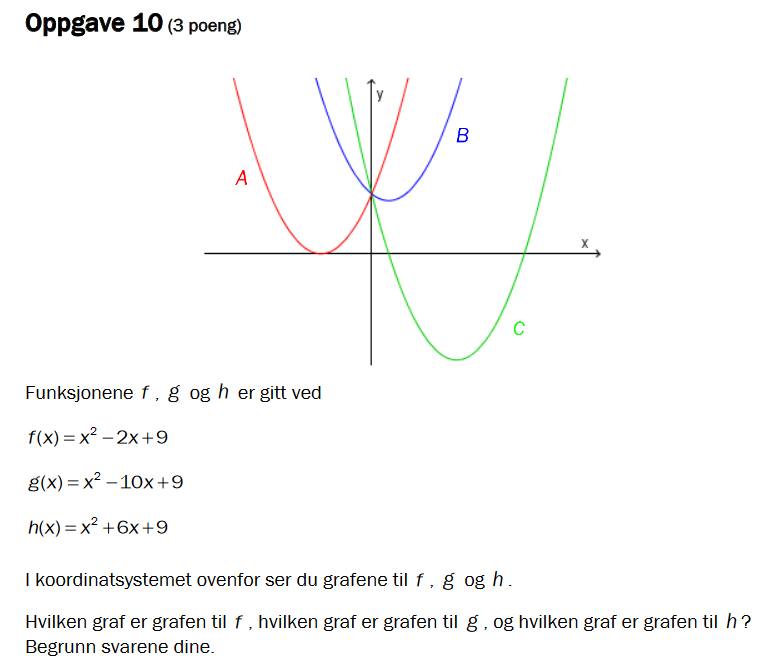
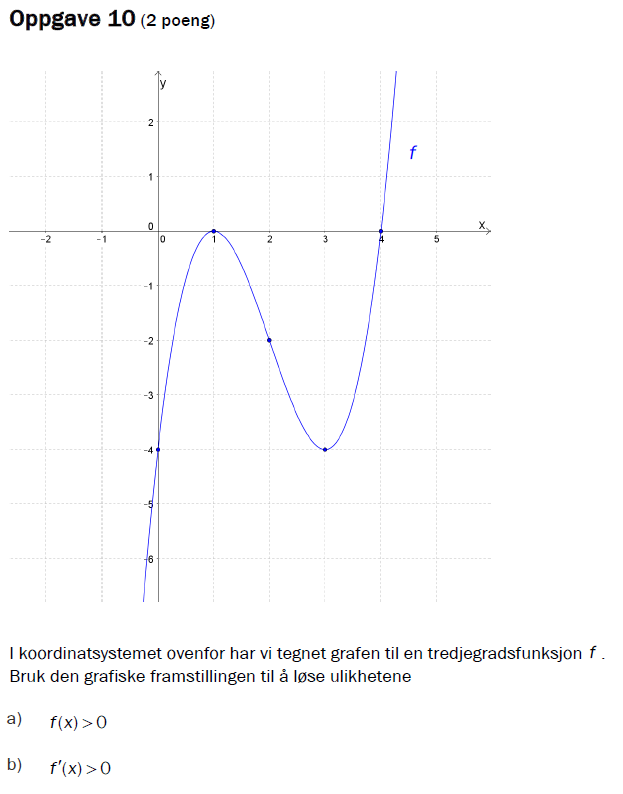
LektorH skrev:Oppgave 10 i år var da ganske enkel? Les rett av, når grafen er positiv er f(x)>0, det er for x>4, og når grafen stiger er f'(x)>0, det er for xe<<-, 1> U <3, ->>. Som Fysikkmann97 sa synes jeg også denne var enklere enn den fra 2016.Bananiel skrev: For 1T så lurer jeg bare på hvordan noen kan rettferdiggjøre dette:
Eksamen 1T våren 2016, oppgave 10 del 1: Eksamen 1T våren 2017, oppgave 10 del 1: Og dette:
Er nullpunktene til grafen egentlig positive? Litt usikker. Takk.
Var det egentlig noen som skjønte oppgave 11 del 1 fra c og nedover?
Eksamen 1T våren 2016, oppgave 7 del 2: Eksamen 1T våren 2017, oppgave 7 del 2:
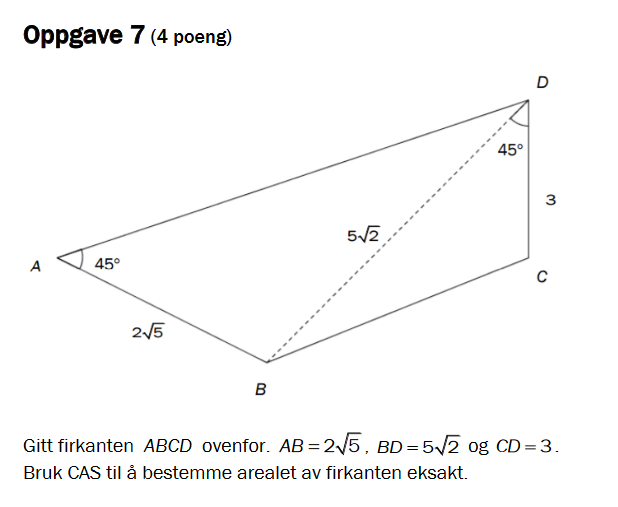
Når det gjelder oppgave 7 var vel årets oppgave litt mer spesiell, men siden a var "vis at" så er vel b grei å finne med formelen for areal av sirkler som bør være kjent, slik Thomas gjorde.
Campus er bra innføring, men det er jo mest en gjennomgang av reglene og helt grunnleggende oppgaver, slik som oppgavene framme i boka. Man må gjøre eksamensoppgaver og sammensatte oppgaver bak i boka.
Hei. Så just på fasiten din. Er helt med på oppgave 11 del 1 inntil e. Jeg har tegnet tangenten i oppgave d, men vet ikke hvordan jeg kan bevise det.mattemarkus skrev:Det er lagt ut løsningsforslag på del 2, så du kan vel rette selv? Så er det bare å spørre hvis noe med løsningsforslaget er uklart?Spiderman98 skrev:Kan noen rette min del 2? Er ganske desperat etter 6eren, og føler at alt i del 2 jeg har gjort bør gi meg alt riktig. Kanskje noen 1 poeng feil for forklaringer. Hva tenker dere?
Hvorfor må f'(1)=-2 for at likningen stemmer? Læreren er usikker på min standpunkt karakter, og vil at jeg skal ta en ekstra prøve imorgen. Jeg tenker oppgaver fra eksamen er aktuelle, så jeg gjør disse. Takk.
-
LektorNilsen
- Descartes

- Innlegg: 438
- Registrert: 02/06-2015 15:59
Tangenten har stigningstall -2, som også må være verdien til den deriverte i tangeringspunktet. Siden tangenten tangerer grafen til (1, f(1))=(1,0), må vi f'(1)=-2.Banan skrev:Hei. Så just på fasiten din. Er helt med på oppgave 11 del 1 inntil e. Jeg har tegnet tangenten i oppgave d, men vet ikke hvordan jeg kan bevise det.mattemarkus skrev:Det er lagt ut løsningsforslag på del 2, så du kan vel rette selv? Så er det bare å spørre hvis noe med løsningsforslaget er uklart?Spiderman98 skrev:Kan noen rette min del 2? Er ganske desperat etter 6eren, og føler at alt i del 2 jeg har gjort bør gi meg alt riktig. Kanskje noen 1 poeng feil for forklaringer. Hva tenker dere?
Hvorfor må f'(1)=-2 for at likningen stemmer? Læreren er usikker på min standpunkt karakter, og vil at jeg skal ta en ekstra prøve imorgen. Jeg tenker oppgaver fra eksamen er aktuelle, så jeg gjør disse. Takk.
Verdien til den deriverte i et punkt er det samme som stigningstallet til tangenten i punktet.
Tusen takk. Det virkelig hjalp. Forstår ikke hvordan jeg ikke skjønte det?! GIdder du å forklare det med konstantleddet også? Hva menes med b?LektorNilsen skrev:Tangenten har stigningstall -2, som også må være verdien til den deriverte i tangeringspunktet. Siden tangenten tangerer grafen til (1, f(1))=(1,0), må vi f'(1)=-2.Banan skrev:Hei. Så just på fasiten din. Er helt med på oppgave 11 del 1 inntil e. Jeg har tegnet tangenten i oppgave d, men vet ikke hvordan jeg kan bevise det.mattemarkus skrev:
Det er lagt ut løsningsforslag på del 2, så du kan vel rette selv? Så er det bare å spørre hvis noe med løsningsforslaget er uklart?
Hvorfor må f'(1)=-2 for at likningen stemmer? Læreren er usikker på min standpunkt karakter, og vil at jeg skal ta en ekstra prøve imorgen. Jeg tenker oppgaver fra eksamen er aktuelle, så jeg gjør disse. Takk.
Verdien til den deriverte i et punkt er det samme som stigningstallet til tangenten i punktet.
-
LektorNilsen
- Descartes

- Innlegg: 438
- Registrert: 02/06-2015 15:59
Tar utgangspunkt i at tangenten er ei rett linje. Generelt kan vi si at likningen til ei rett linje er gitt ved [tex]y=a\cdot x+b[/tex], der a er stigningstallet og b er konstantleddet, altså y-verdien til skjæringspunktet med y-aksen (hvis x=0 vil første leddet være lik 0 og vi har kun y=b). I nest siste deloppgave skal vi skissere en tangent og finne likningen til denne. Vi ser at likningen skal være [tex]y=-2\cdot x+2[/tex], så det er det vi må vise i siste deloppgave. Vi "sjekker" at vi har riktig stigningstall ved å se at f'(1)=-2 (som allerede er forklart), men vi må også sjekke at vi har riktig konstantledd. Når vi har riktig vedi for a og kjenner et punkt som ligger på tangenten, kan vi sette inn verdien vår for a sammen med x- og y-verdiene til det kjente punktet i likningen vår. Da sitter vi igjen med en likning med én ukjent, nemlig b. Vi løser denne og ser at b=2, så da må likningen vi fant i forrige deloppgave stemmeTusen takk. Det virkelig hjalp. Forstår ikke hvordan jeg ikke skjønte det?! GIdder du å forklare det med konstantleddet også? Hva menes med b?
Tusen takk! Det ga så mye mening. Takk for at du svarte så fort. Har prøve kl. 11.LektorNilsen skrev:Tar utgangspunkt i at tangenten er ei rett linje. Generelt kan vi si at likningen til ei rett linje er gitt ved [tex]y=a\cdot x+b[/tex], der a er stigningstallet og b er konstantleddet, altså y-verdien til skjæringspunktet med y-aksen (hvis x=0 vil første leddet være lik 0 og vi har kun y=b). I nest siste deloppgave skal vi skissere en tangent og finne likningen til denne. Vi ser at likningen skal være [tex]y=-2\cdot x+2[/tex], så det er det vi må vise i siste deloppgave. Vi "sjekker" at vi har riktig stigningstall ved å se at f'(1)=-2 (som allerede er forklart), men vi må også sjekke at vi har riktig konstantledd. Når vi har riktig vedi for a og kjenner et punkt som ligger på tangenten, kan vi sette inn verdien vår for a sammen med x- og y-verdiene til det kjente punktet i likningen vår. Da sitter vi igjen med en likning med én ukjent, nemlig b. Vi løser denne og ser at b=2, så da må likningen vi fant i forrige deloppgave stemmeTusen takk. Det virkelig hjalp. Forstår ikke hvordan jeg ikke skjønte det?! GIdder du å forklare det med konstantleddet også? Hva menes med b?
Løsningsforslag. Hyl ut om slurvefeil eller feil...
- Vedlegg
-
- 1T_eksamen_v2017_LF.pdf
- (246.94 kiB) Lastet ned 579 ganger
Hadde just prøven. Vi fikk hele dette eksamensettet. Så glad at jeg gjorde dette på forhånd. Tusen takk for all hjelpen!Banan skrev:Tusen takk! Det ga så mye mening. Takk for at du svarte så fort. Har prøve kl. 11.LektorNilsen skrev:Tar utgangspunkt i at tangenten er ei rett linje. Generelt kan vi si at likningen til ei rett linje er gitt ved [tex]y=a\cdot x+b[/tex], der a er stigningstallet og b er konstantleddet, altså y-verdien til skjæringspunktet med y-aksen (hvis x=0 vil første leddet være lik 0 og vi har kun y=b). I nest siste deloppgave skal vi skissere en tangent og finne likningen til denne. Vi ser at likningen skal være [tex]y=-2\cdot x+2[/tex], så det er det vi må vise i siste deloppgave. Vi "sjekker" at vi har riktig stigningstall ved å se at f'(1)=-2 (som allerede er forklart), men vi må også sjekke at vi har riktig konstantledd. Når vi har riktig vedi for a og kjenner et punkt som ligger på tangenten, kan vi sette inn verdien vår for a sammen med x- og y-verdiene til det kjente punktet i likningen vår. Da sitter vi igjen med en likning med én ukjent, nemlig b. Vi løser denne og ser at b=2, så da må likningen vi fant i forrige deloppgave stemmeTusen takk. Det virkelig hjalp. Forstår ikke hvordan jeg ikke skjønte det?! GIdder du å forklare det med konstantleddet også? Hva menes med b?
Jeg regnet gjennom del 1 i går, det tok litt over en time, som var mer tid enn jeg brukte på del 1 av R2-eksamen. Jeg har regnet gjennom R1, R2 og S2 tidligere, og alle de var ganske enkle i år, men denne hadde noen småtriks til dere. Jeg vil si at 1T var den vanskeligste eksamenen av de jeg har gjort i år (sånn i forhold til pensum, så klart). Det er uansett bare en teoretisk problemstilling, ingen av mine kom opp i skriftlig.Spode skrev:Hva tenker dere om 1T eksamen? Vanskelig, lett?
Symmetrilinja var sikkert vrien for mange? Jeg har lært mine elever at andregradsfunksjoner er symmetriske rundt ekstremalpunktet, men jeg vet ikke om de har fått med seg at ei linje kan være x=a, og ikke bare y=ax+b. De to tangentoppgavene der var også litt vriene.
Ellers virket del 1 grei nok, selv om det tok litt tid. Jeg likte oppgave 12, det var en bra måte å sjekke at elevene kan de trigonometriske setningene uten at matematikken ble for vrien.
Oppgave 3 på del 2 var kanskje forvirrende? Vi har bare jobbet med tabeller i min klasse, ikke med å hente verdiene ut fra en graf. Det kunne i hvert fall vært punkter i stedet for ei linje, så hadde det vært lettere å se hva man skulle gjøre.
Uttrykket "stasjonært punkt" i oppgave 6 på del 2 har jeg heller ikke brukt, det er nok arbeid å få folk til å huske at "ekstremalpunkt" betyr topp eller bunn. Forhåpentligvis skjønte dere det når neste del var å vise om det var topp, bunn eller terrassepunkt. Har noen lært begrepet stasjonært punkt på skolen? Jeg må tydeligvis ta det inn til neste år...
Ellers var det stort sett greit tror jeg. Jeg har tatt ut noen av oppgavene fra del 2 til muntligforberedelse, så får vi se om elevene mine ser hva de skal gjøre.
(Og så oppgave 7: 98% av elevene leser en form for aviser? Det høres... mye ut.)