Trigonometriske likninger

[Jibe42]

Hei!

Jeg har begynt med trigonometriske likninger og kom borti denne oppgaven
: [tex]4\sin^2 x= 3x \in [0^{\circ}, 360^{\circ}][/tex]

Jeg kommer så langt som å finne første løsning: [tex]x_{0} = 60^{\circ}[/tex]
Vi har fått beskjed om å bruke enhetssirkelen for å finne de resterende løsninger. Hvordan gjør man dette? Har lest i boken, men skjønner ikke stort :/

Er det mulig å få en ''grundig'' forklaring ?

[jonasgilje]

Er du sikker på at likningen er kopiert skikkelig? Den eneste løsningen er [tex]x=0[/tex].

[Dolandyret]

Hei!

Jeg har begynt med trigonometriske likninger og kom borti denne oppgaven
: [tex]4\sin^2 x= 3x \in [0^{\circ}, 360^{\circ}][/tex]

Jeg kommer så langt som å finne første løsning: [tex]x_{0} = 60^{\circ}[/tex]
Vi har fått beskjed om å bruke enhetssirkelen for å finne de resterende løsninger. Hvordan gjør man dette? Har lest i boken, men skjønner ikke stort :/

Er det mulig å få en ''grundig'' forklaring ?

[tex]4sin^2x=3[/tex]
[tex]sin^2x=\frac{3}{4}[/tex]
[tex]sinx=\sqrt{\frac{3}{4}}=\frac{\sqrt3}{2}[/tex]
[tex]x=sin^{-1}(\frac{\sqrt3}{2})=60^{\circ}[/tex]

Fra trigonometrien har vi at [tex]sin=\frac{mot}{hyp}[/tex] og [tex]cos=\frac{hos}{hyp}[/tex]. I enhetssirkelen er radiusen alltid én og [tex]radius=hypotenus[/tex] i de rettvinklede trekantene som formes når du uttrykker noe ved sinus eller cosinus. Dette vil derfor si at i de rettvinklede trekantene så er [tex]sin=\frac{mot}{hyp}=\frac{mot}{1}=mot[/tex] og [tex]cos=\frac{hos}{hyp}=\frac{hos}{1}=hos[/tex].
Illustrert ved tegning:

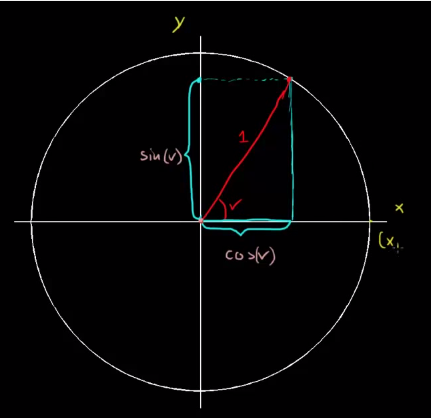
enhetssirkelen.png (51.54 kiB) Vist 3794 ganger

Vi kan derfor skrive punktet hvor hypotenusen treffer sirkelbuen som (cosx,sinx). ved v=0 ser vi at vi har koordinatene (1,0), ved v=90 har vi (0,1), ved v=180 har vi (-1,0) og ved v=270 har vi (0,-1). Hva dette sier oss er at: cos(1)=0grader og sin(0)=0grader, cos(1)=90grader og sin(0)=90grader, cos(-1)=180grader og sinus(0)=180grader, cos(0)=270grader og sin(-1)=270grader.
Det jeg prøver å illustrere ved å si dette, er at hver verdi av cosinus og sinus kan uttrykkes ved to forskjellige grader. Vi ser jo f.eks. at sin(0)=0grader og sin(0)=180grader. Sinusfunksjonen speiles om y-aksen. Dvs. at om vi har en vinkel i første kvadrant, på f.eks. 45grader, så har vi også en vinkel i 180-45=135grader. For cosinusfunksjonen er dette litt annerledes, da den speiles om x-aksen. En vinkel på 45 grader vil derfor ha samme verdi for cosinus som en vinkel på 360-45=315grader.

Kort og godt; vi har funnet ut at vi har en vinkel lik 60grader, vi har med en sinusfunksjon å gjøre, derfor må det også være en vinkel som gir samme verdi i 180-60=120grader.

Vi har da funnet ut at løsningene i det første omløpet av enhetssirkelen, altså [tex]x\in[0^{\circ},360^{\circ}][/tex] har [tex]L=\left \{ 60^{\circ},120^{\circ} \right \}[/tex]

Dårlig forklart av meg, men her er en video som forklarer alt litt bedre:
https://www.youtube.com/watch?v=DzsMTkcUkZs

[Jibe42]

Kort og godt; vi har funnet ut at vi har en vinkel lik 60grader, vi har med en sinusfunksjon å gjøre, derfor må det også være en vinkel som gir samme verdi i 180-60=120grader.

Vi har da funnet ut at løsningene i det første omløpet av enhetssirkelen, altså [tex]x\in[0^{\circ},360^{\circ}][/tex] har [tex]L=\left \{ 60^{\circ},120^{\circ} \right \}[/tex]

Dårlig forklart av meg, men her er en video som forklarer alt litt bedre:
https://www.youtube.com/watch?v=DzsMTkcUkZs

WoW! Skal love deg at det var tusen ganger bedre enn boken og læreren!

I og med at det er [tex]X \in [0^{\circ},360^{\circ}][/tex] får jeg at neste er 240 grader, men er veldig usikkert på om det er rett...

Hva skal man gjøre dersom man har en tangens funksjon?

[Dolandyret]

Kort og godt; vi har funnet ut at vi har en vinkel lik 60grader, vi har med en sinusfunksjon å gjøre, derfor må det også være en vinkel som gir samme verdi i 180-60=120grader.

Vi har da funnet ut at løsningene i det første omløpet av enhetssirkelen, altså [tex]x\in[0^{\circ},360^{\circ}][/tex] har [tex]L=\left \{ 60^{\circ},120^{\circ} \right \}[/tex]

Dårlig forklart av meg, men her er en video som forklarer alt litt bedre:
https://www.youtube.com/watch?v=DzsMTkcUkZs

WoW! Skal love deg at det var tusen ganger bedre enn boken og læreren!

I og med at det er [tex]X \in [0^{\circ},360^{\circ}][/tex] får jeg at neste er 240 grader, men er veldig usikkert på om det er rett...

Hva skal man gjøre dersom man har en tangens funksjon?

Neste blir ikke 240 grader, vi har bare at svarene blir 60- og 120grader i akkurat denne oppgaven.
Det du gjør, når du har funnet de to vinklene, er at du kan legge til 360 grader for å finne flere løsninger, men siden vi her har begrenset x for [tex]x\in[0^{\circ},360^{\circ}][/tex], så vil 60+360=420 og 120+360=480, være utenfor definisjonsmengden. Men om du hadde hatt at [tex]x\in[0^{\circ},720^{\circ}][/tex], så hadde vi hatt 4 løsninger; [tex]L=\left \{ 60^{\circ},120^{\circ},60^{\circ}+360^{\circ},120^{\circ}+360^{\circ} \right \}=\left \{ 60^{\circ},120^{\circ},420^{\circ},480^{\circ} \right \}[/tex]. Dette ser du om du ser på enhetssirkelen, en vinkel lik 60grader er jo like stor om du har gått en ekstra runde rundt sirkelen.

Generelt har vi at: [tex]L=x+n360^{\circ}[/tex] [tex]n\in Z[/tex] hvor Z er alle heltall, altså [tex]\leftarrow...-4,-3,-2,-1,0,1,2,3,4...\rightarrow[/tex]. Så si at denne oppgaven ikke hadde hatt noen begrensninger, da ville løsningen din blitt:
[tex]L=60^{\circ}+n360^{\circ}\wedge L=120^{\circ}+n360^{\circ}[/tex] [tex]n\in Z[/tex]


Tangensfunksjonen ja, den er litt "merkelig". Fra trigonometrien har vi at [tex]tan=\frac{sin}{cos}[/tex]. Dette er jo greit nok, men siden for visse grader, er cosinus=0, og da vil tangensfunksjonen være udefinert. Dette er ved 90- og 270grader. En tangensfunksjon gjentar seg alltid for hver 180'ende grad. dvs. at om vi har funnet ut at løsningen for x i en tangensfunksjon er 30grader, så har vi at: [tex]L=30^\circ+n180^\circ[/tex] [tex]n\in Z[/tex]