Løsning del 1 utrinn Vår 23
Diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
To likninger med to ukjente.
x = pris sjokolade og y = pris slikkepinne.
Bilde 1 gir:
2y + 2x =32 (deler alle ledd på 2 og flytter trekker fra x på begge sider)
y = 16 - x
Bilde 2 gir:
4y + 2x = 44 (setter inn for y)
4(16-x) +2x = 44
64 -2x = 44
x=10
Da blir y = 16 - 10 =6
Sjokoladen koster 10 kroner og slikkepinnen koster 6 kroner.
Alternativt kan man tenke: Forskjellen på bildene er to slikkepinner og 12 kroner, da må en slikkepinne koste 6 kroner (som er det eneste de spør om).
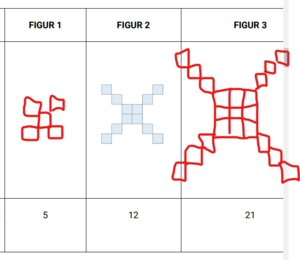
Oppgave 2
a)
b)
Dersom vi kaller figurnummeret for n: Kvadratet i midten består av $n^2$ småkvadrater. Så er det fire armer med n kvadrater.
Formelen blir da $B(n)= n^2 + 4n$
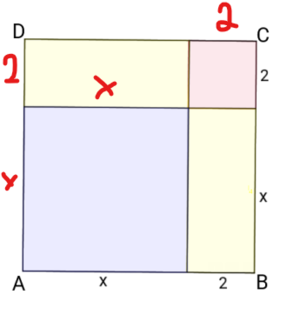
Oppgave 3
Ett gult felt har areal 2x. To gule felt har areal 4x.
Rosa kvadrat har areal 4.
Lilla kvadrat har areal $x^2$
Arealet av det store kvadratet med sidekanter (x+2) blir:
$(x+2)(x+2)= x^2+ 4x + 4$, som er det samme om vi legger sammen arealene av de fire små figurene. Dette er første kvadratsetning.
Oppgave 4
a)
Typetall er 62 (flest like verdier)
Median er 61, gjennomsnittet av tall nr. 5 og nr. 6.
Gjennomsnittet er summen av alle målingene, delt på ti. Det er 52.
b)
Måling 2 og 4 skiller seg ut og drar snittet ned. Både median og typetall gir et godt bilde av hastigheten. Jeg ville brukt medianverdien fordi da vet jeg at det er like mange målinger under som over.
Oppgave 5
Oppgave 6
Når det har gått en halv time (0,5) er tilbakelagt strekning 30 km. Gjennomsnittshastigheten er da 60 km/t. Stigningstallet er 60 i denne funksjonen som viser tilbakelagt strekning som funksjon av tid.
Oppgave 7
979 kroner er nesten 1000 kroner. $\frac{200}{1000}$ er 0,2 , så han fikk ca. 20% avslag.