2P-Y 2013 vår LØSNING
Del 1
Oppgave 1
a)
Finn median:
Sorterer observasjonene: $1_{(1)} \;\; 1_{(2)} \;\; 1_{(3)} \;\; 2_{(4)} \;\; 2_{(5)} \;\; 3_{(6)} \;\; 3_{(7)} \;\; 4_{(8)} \;\; 5_{(9)} \;\; 5_{(10)}$
Finner antall observasjoner: $N = 10$
Finner midtpunktet: ${N + 1 \over 2} = {10 + 1 \over 2} = 5.5$
Fordi det er et partall antall observasjoner er medianen lik gjennomsnittet av de to verdiene som ligger på hver sin side av midtpunktet
Medianen er gjennomsnittet av verdiene nummer 5 og 6. ${2 + 3 \over 2 }= 2.5$
Finner gjennomsnitt:
Finner summen av observasjonsverdiene: $S=1+5+3+3+5+2+1+4+1+2=27$
Finner antall observasjoner: $N=10$
Gjennomsnittet er da: ${S \over N} = {27 \over 10} = 2.7$
Finn typetall:
Teller opp verdiene og lager en frekvenstabell:
| Verdi $x$ | Frekvens $f$ |
|---|---|
| $1$ | $3$ |
| $2$ | $2$ |
| $3$ | $2$ |
| $4$ | $1$ |
| $5$ | $2$ |
Ser i tabellen og finner de hyppigst forekommende verdiene
Typetall(ene) er: 1
b)
| Verdi x | Frekvens f | Kumulativ frekvens |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 2 | 3+2 = 5 |
| 3 | 2 | 5+2 = 7 |
| 4 | 1 | 7+1 = 8 |
| 5 | 2 | 8 + 2 = 10 |
Oppgave 2
$0,075 \cdot 2000000 = (7,5 \cdot 10^{-2}) \cdot (2 \cdot 10^6) = = 7,5 \cdot 2 \cdot 10^{-2+6} = 15 \cdot 10^{4} = 1,5 \cdot 10^1 \cdot 10^{4} =1,5 \cdot 10^{5}$
Oppgave 3
A: $\frac{15 \cdot 5^{-1}}{2^2} = \frac{3 \cdot 5 \cdot 5^{-1}}{2^2} = \frac{3}{4} $
B: $\frac{1}{6^{-2}\cdot 3 \cdot 15} = \frac{6^2}{ 3 \cdot 3 \cdot 5} = \frac{36}{ 9 \cdot 5} = \frac{36}{ 9} \cdot \frac{1}{5} = 4 \cdot \frac{1}{5} = \frac{4}{5}$
Fordi $\frac{4}{5} > \frac{3}{4}$ har brøken B størst verdi.
Oppgave 4
a)
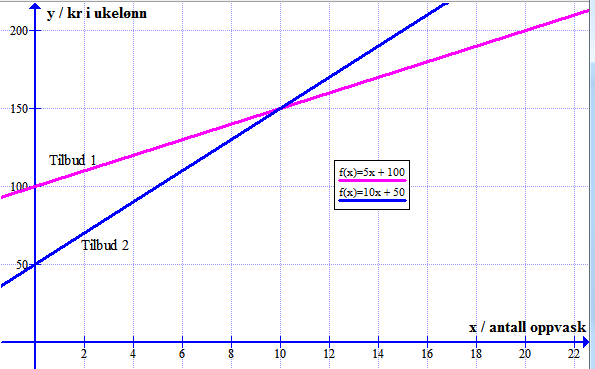
Tilbud 1: $y = 5x + 100$
Tilbud 2: $y = 10x + 50$
b)
Ettersom dette er del 1 av eksamen, må denne grafen skisseres for hånd, men jeg bruker her Graph
Ser av grafen at det lønner seg for Sigvald med tilbud 1 dersom han vasker opp mindre enn 10 ganger i uka. Vi vet ikke hvor ofte de vasker opp i familien, men hvis de for eksempel vasker opp en gang om dagen, så lønner det seg for Sigvald med Tilbud 1.
Oppgave 5
| Plassverdisystem med grunntall 10 | Plassverdisystem med grunntall 2 |
|---|---|
| $43$ | $101011_2$ |
| $26$ | $11010_2$ |
Konverterer $101011_{(2)}$ til 10-tallsystemet:
${{\color{red}{1}\cdot 2^{5}+\color{red}{0}\cdot 2^{4}+\color{red}{1}\cdot 2^{3}+\color{red}{0}\cdot 2^{2}+\color{red}{1}\cdot 2^{1}+\color{red}{1}\cdot 2^{0}} = \\{32+0+8+0+2+1}} = {\color{red}{ \underline{ \underline{43_{(10)} } } }}$
Konverterer $26_{(10)}$ til 2-tallsystemet:
${26_{(10) } } = {16+8+0+2+0}= {{\color{red}{1}\cdot 2^{4}+\color{red}{1}\cdot 2^{3}+\color{red}{0}\cdot 2^{2}+\color{red}{1}\cdot 2^{1}+\color{red}{0}\cdot 2^{0}}} = {\color{red}{ \underline{ \underline{11010_{(2)} } } }}$
Oppgave 6
a)
$f(x) = 100 000 \cdot 0,9^x$
b)
Graf C tilhører f.
Vi ser at graf A er en rett linje, men $f(x)$ er en eksponensialfunksjon.
Graf C synker raskest i starten, men etterhvert som bilen blir billigere så går den mindre ned i verdi hvert år. Prisen synker med 10% hvert år, og det blir 10% av et mindre og mindre beløp.
Oppgave 7
| Inntekt (i 1000 kroner) | Klassemidtpunkt $x_m$ | Antall personer$f$ | Klassesum $f \cdot x_m$ |
| $[300 , 400\rangle $ | $350$ | $20$ | $7000$ |
| $[400 , 500\rangle $ | $450$ | $20$ | $9000$ |
| $[500 , 700\rangle $ | $600$ | $10$ | $6000$ |
| $N=50$ | $S=22000$ |
Gjennomsnittet er omtrent: $ g = \frac{S}{N} = {\frac{22000}{ 50}} = {440}$ tusen kroner
Oppgave 8
Løsning med krysstabell
a)
| Vært i USA | Ikke vært i USA | Totalt | |
|---|---|---|---|
| Vært i Spania | 4 | 7 | 11 |
| Ikke vært i Spania | 4 | 5 | 9 |
| Totalt | 8 | 12 | 20 |
b)
$P(\text{Eleven har vært både i USA og i Spania}) = {4 \over 20} = {2 \over 10} = 0.2$
c)
$P(\text{Eleven har vært i Spania gitt at han ikke har vært i USA}) = {7 \over 12}$
Del 2
Oppgave 1
a)
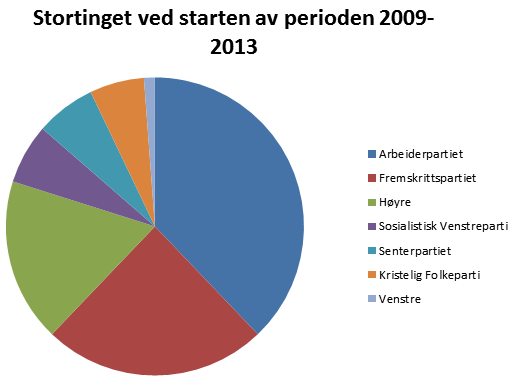
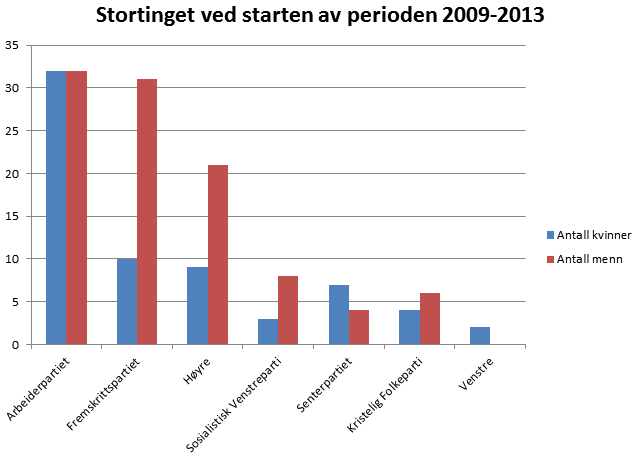
Bruker Excel for å tegne sektordiagrammet..
b)
Oppgave 2
a)
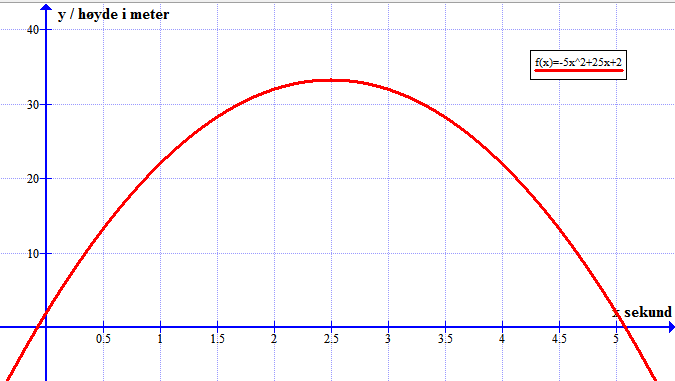
Bruker programmet Graph Bruker funksjonen: "Sett inn funksjon".
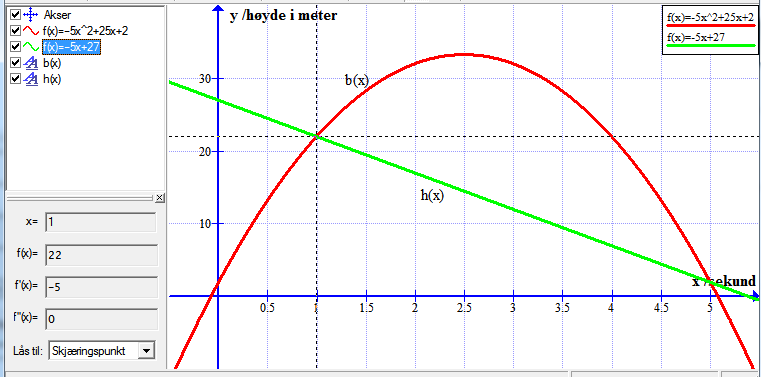
b)
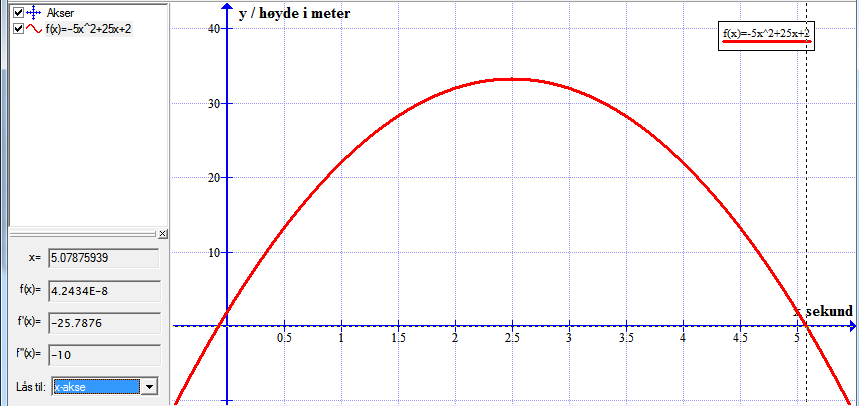
Bruker funksjonen: Beregn => "Lås til x-aksen" for å finne når ballen treffer bakken.
Leser av grafen at den treffer bakken ved tid 5.1 sekunder.
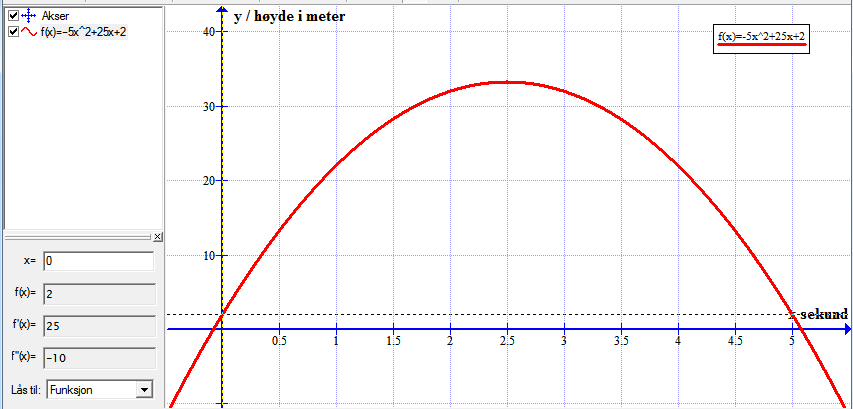
Bruker funksjonen: Beregn => "Lås til funksjon" for å finne høyden når ballen kastes. Velger x=0.
Leser av grafen at den er 2 meter over bakken når den kastes.
c)
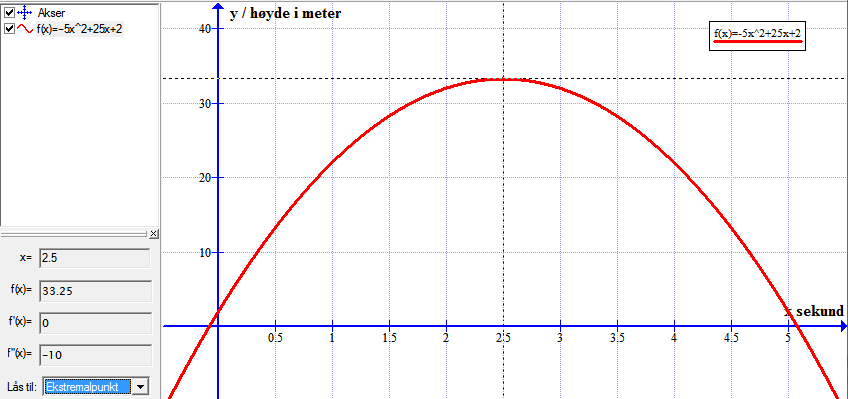
Bruker funksjonen: Beregn => "Lås til ekstremalpunkt" for å finne toppunktet.
Leser ut av grafen at ballen når sitt høyeste nivå etter 2.5 sekunder. Da er ballen 33.25 meter over bakken.
d)
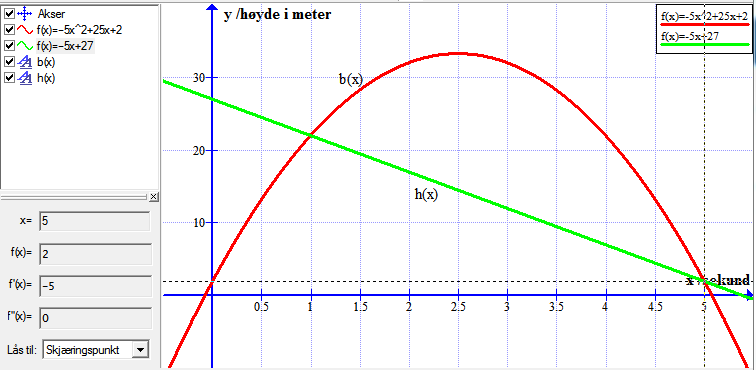
Bruker funksjonen: "Sett inn funksjon" for å tegne $h(t)$
Bruker funksjonen: Beregn => "Lås til skjæringspunkt" og klikker i nærheten av de to skjæringspunktene.
Leser ut av grafen at skjæringspunktene er $(1,22)$ og $(5,2)$. Det vil si at ballen og heisen er like høyt over bakken etter 1 sekund og etter 5 sekunder. Dersom de er på samme sted kan ballen treffe heisen.
Skjæringspunkt 1:
Skjæringspunkt 2:
Oppgave 3
a)
Vinnertid 1968: 123.4
Vinnertid 2010:105,57
$\frac{105,57}{123,4} = 0.86$
$1 - 0.86 = 0.14$
Vinnertiden sank med 14% fra 1968 til 2010.
b)
Bruker 2P-kalkulatoren. Funksjon: Verdiliste => Gjennomsnitt.
Gjennomsnitt1968: 125.06 sekunder
Gjennomsnitt 2010: 106.36 sekunder
Utregning for gjennomsnitt 1968 (ikke nødvendig å vise for å få full uttelling på oppgaven):
Finner summen av observasjonsverdiene: $S = 123.4 + 125 + 125 + 125.1 + 125.2 + 125.2 + 125.5 + 126.1 = 1\space 000.5$
Finner antall observasjoner: $N = 8$
Gjennomsnittet er da: ${S \over N} = {1\space 000.5 \over 8} = 125.06$
Utregning for gjennomsnitt 2010 (ikke nødvendig å vise for å få full uttelling på oppgaven):
Finner summen av observasjonsverdiene: $S = 105.57 + 106.1 + 106.13 + 106.42 + 106.47 + 106.69 + 106.76 + 106.77 = 850.91$
Finner antall observasjoner: $N = 8$
Gjennomsnittet er da: ${S \over N} = {850.91 \over 8} = 106.36$
c)
Bruker 2P-kalkulatoren. Funksjon: Verdiliste => Standardavvik.
Standardavvik 1968: 0.714 sekunder
Standardavvik 2010: 0.387 sekunder
Årsaken til at standardavviket er større i 1968 enn i 2010 er at det er større forskjell mellom de beste og de dårligste i 1968 enn i 2010. Det er er jevnere og høyere nivå i 2010. Det er spesielt 2 løpere som skiller seg ut i 1968: Kees Verkerk og Eduard Matusevitsj. Verkerk er mye bedre enn de andre, og Matusevitsj er mye dårligere enn de andre. Hvis vi fjerner disse to fra resultatlista, så vil forskjellen i standardavviket bli en del mindre.
Utregning for standardavvik 1968 (ikke nødvendig å vise): Finner først gjennomsnittet:
Finner summen av observasjonsverdiene: $S = 123.4 + 125 + 125 + 125.1 + 125.2 + 125.2 + 125.5 + 126.1 = 1\space 000.5$
Finner antall observasjoner: $N = 8$
Gjennomsnittet er da: ${S \over N} = {1\space 000.5 \over 8} = 125.06$
Bruker gjennomsnittet for å regne ut variansen:
| Verdi $x$ | $(x-g)^2$ |
|---|---|
| $123.4$ | $(123.4-125.06)^2 = (-1.66)^2 = 2.76$ |
| $125$ | $(125-125.06)^2 = (-0.06)^2 = 0.00391$ |
| $125$ | $(125-125.06)^2 = (-0.06)^2 = 0.00391$ |
| $125.1$ | $(125.1-125.06)^2 = 0.0375^2 = 0.00141$ |
| $125.2$ | $(125.2-125.06)^2 = 0.137^2 = 0.0189$ |
| $125.2$ | $(125.2-125.06)^2 = 0.137^2 = 0.0189$ |
| $125.5$ | $(125.5-125.06)^2 = 0.437^2 = 0.191$ |
| $126.1$ | $(126.1-125.06)^2 = 1.04^2 = 1.08$ |
| $A= 4.08$ |
Variansen er: $ \frac{A}{ N}=\frac{4.08}{ 8}=0.51$ Bruker variansen for å regne ut standardavvik
Standardavviket er: $ \sqrt{\text{Variansen}} = \sqrt{0.51} = 0.714$
Utregning for standardavvik 2010 (ikke nødvendig å vise):
Finner først gjennomsnittet:
Finner summen av observasjonsverdiene: $S = 105.57 + 106.1 + 106.13 + 106.42 + 106.47 + 106.69 + 106.76 + 106.77 = 850.91$
Finner antall observasjoner: $N = 8$
Gjennomsnittet er da: ${S \over N} = {850.91 \over 8} = 106.36$
Bruker gjennomsnittet for å regne ut variansen
| Verdi $x$ | $(x-g)^2$ |
|---|---|
| $105.57$ | $(105.57-106.36)^2 = (-0.79)^2 = 0.63$ |
| $106.1$ | $(106.1-106.36)^2 = (-0.26)^2 = 0.0696$ |
| $106.13$ | $(106.13-106.36)^2 = (-0.23)^2 = 0.0546$ |
| $106.42$ | $(106.42-106.36)^2 = 0.0563^2 = 0.00316$ |
| $106.47$ | $(106.47-106.36)^2 = 0.106^2 = 0.0113$ |
| $106.69$ | $(106.69-106.36)^2 = 0.326^2 = 0.106$ |
| $106.76$ | $(106.76-106.36)^2 = 0.396^2 = 0.157$ |
| $106.77$ | $(106.77-106.36)^2 = 0.406^2 = 0.165$ |
| $A= 1.2$ |
Variansen er: $ \frac{A}{ N}=\frac{1.2}{ 8}=0.15$
Bruker variansen for å regne ut standardavvik
Standardavviket er: $ \sqrt{\text{Variansen}} = \sqrt{0.15} = 0.387$
Oppgave 4
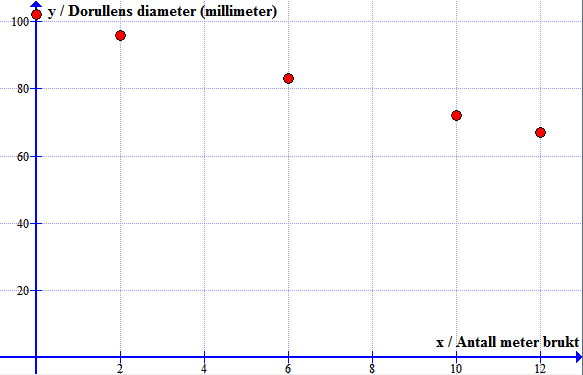
a)
Bruker programmet Graph Bruker funksjonen: "Sett inn punktliste".
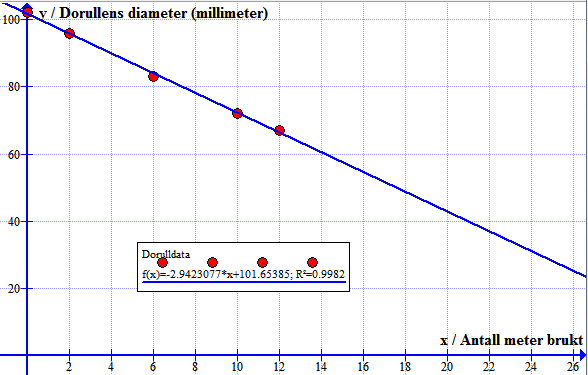
b)
Bruker funksjonen: "Sett inn trendlinje" => Lineær.
Finner at funksjonen $f(x) = 2.9 x + 102$ passer godt med punktene fra oppgave a.
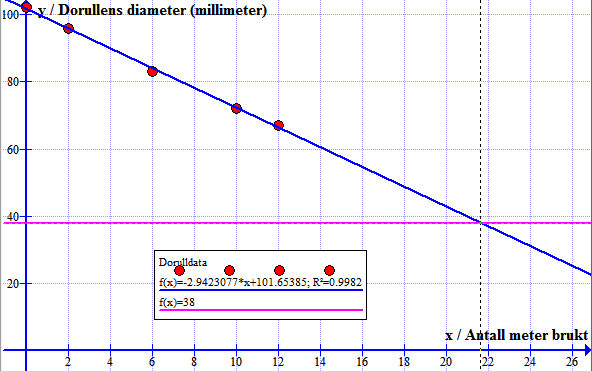
c)
Bruker funksjonen: Sett inn funksjon y=38. Beregn => "lås til skjæringspunkt"
Ser at dorullen er tom når man har brukt 21.6 meter. Dorullen inneholder altså 21.6 meter papir.
d)
$160 \text{ark.} \cdot 14 \text{cm} =160 \cdot 0.14 m = 22.4 \text{meter}$
Modellen sier at det er 21.6 meter på rullen. Det som står på pakken og modellen stemmer altså godt.
Oppgave 5
a)
I en lineær modell synker verdien med et fast beløp hvert år. I oppgaven står det at det årlige verditapet er 25780 kr dermed er det en lineær modell. For å kontrollere kan vi se at fra 2006 til 2011 er det 5 år. $25780 kr \cdot 5 = 128900 kr$ som er oppgitt som det totale verditapet.
Modellen er: $f(x) = 299990 - 25780x$
b)
Løsningsalternativ 1
Forsøker meg fram på kalkulatoren for å finne det årlige verditapet. Vet at prisen etter 5 år er $299990 \cdot k^5$ og forsøker med forskjellige verdier for k.
$299990 \cdot 0.88^5 = 158314 kr$
$299990 \cdot 0.89^5 = 167516 kr$
$299990 \cdot 0.90^5 = 177141 kr$
Ser at vekstfaktoren som passer best er mellom 0.89 og 0.90. Bruker 0.89. Da er den prosentvise nedgangen på $1 - 0.89 = 0.11 = 10%$
Den eksponentielle modellen er da $f(x) = 299990 \cdot 0.89^x$
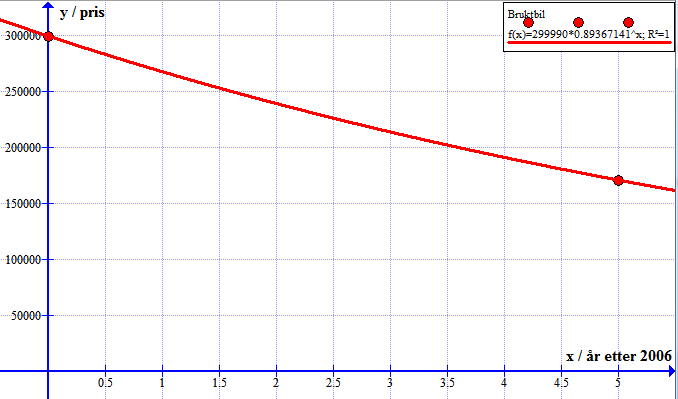
Løsningsalternativ 2 Bruker Graph, og setter inn de to kjente punktene, og bruker så funksjonen "sett inn trendlinje" for å finne en eksponentialfunksjon som passer til observasjonene.
Den eksponentielle modellen er da $f(x) = 299990 \cdot 0.893^x$
Løsningsalternativ 3
$299990 \cdot x^5 = 171000$
$x^5 = {171000 \over 299990 }$
$x^5 = 0.57$
$x = \sqrt[5]{0.57}=0.893$
Den eksponentielle modellen er da $f(x) = 299990 \cdot 0.893^x$
c)
Den lineære modellen: $f(7) = 299990 - 25780 \cdot 7 = 119530 kr$
Den eksponentielle modellen: $f(7) = 299990 \cdot 0.89^7 = 132689.58 kr$