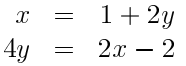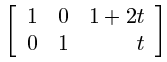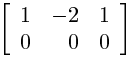Oppgave:
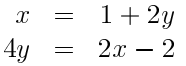
Svar:
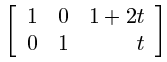
Jeg får dette som svar:
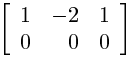
Og den raden med bare 0ere gjør vel at denne matrisen har uendelig med løsninger? Hva er greia med t'en, og hvordan i all verden gikk det fra å være 3 kolonner til 4 kolonner?
Moderatorer: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa