Side 1 av 1
Geometri og areal
Lagt inn: 02/11-2017 20:24
av Janhaa
Den lille sirkelen har senter i [tex]\,C_1\,[/tex]og radius 3. Mens den store sirkelen har senter i [tex]\,C_2\,[/tex]og radius 12.
Linjene l og m går gjennom [tex]\,C_1\,[/tex]og tangerer den store sirkelen i punktene P og Q. Hva er arealet av firkanten
[tex]C_1PC_2Q\,[/tex]?
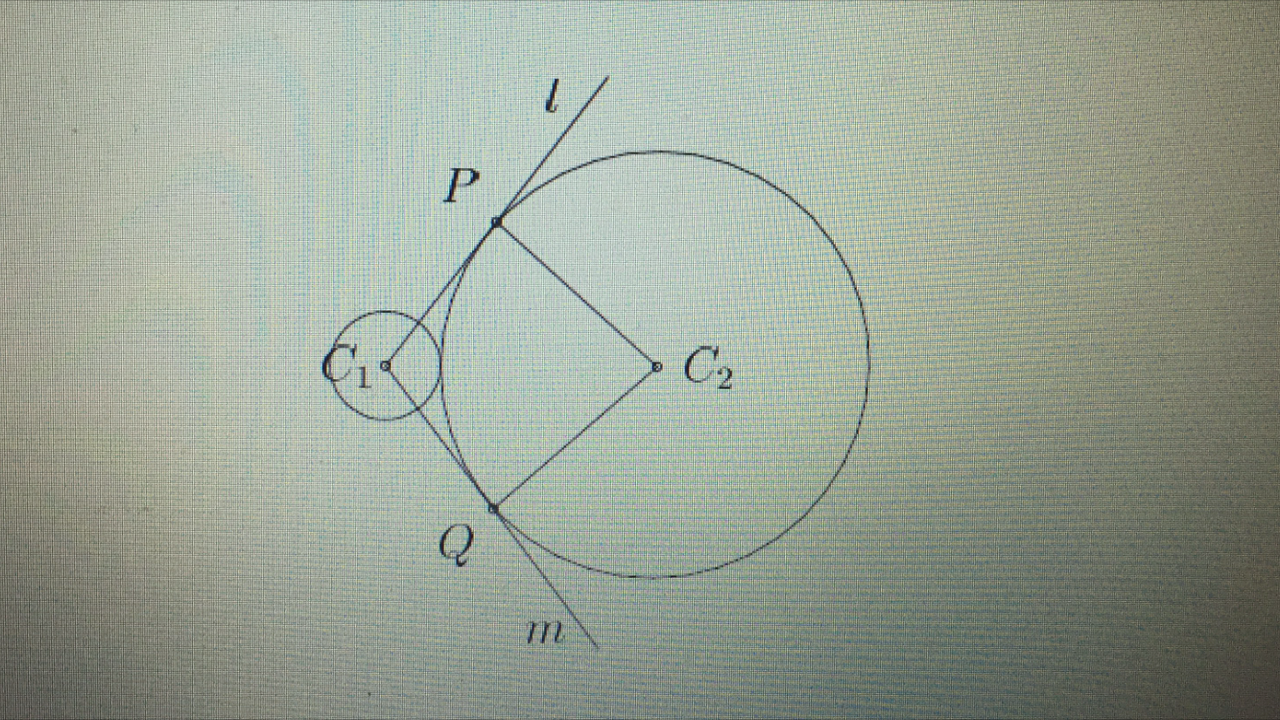
- sirkler-firkant-areal.PNG (1.83 MiB) Vist 2640 ganger
(ble litt stort bilde).
Re: Geometri og areal
Lagt inn: 02/11-2017 20:37
av OYV
C[tex]_1[/tex]C[tex]_2[/tex] = r + R = 3 + 12 = 15
C[tex]_2[/tex]P = R = 12
Da er C[tex]_1[/tex]P = 9 ( Pytagoras læresetning )
Elles registrerer vi at P og Q ligger symmetrisk om de to sirkelsentra.
Areal (firkant ) = 2 * areal(trekant C[tex]_1[/tex]C[tex]_2[/tex]P ) = 2 * 9 * 12/2 = 108
Re: Geometri og areal
Lagt inn: 03/11-2017 17:01
av Markus
Enig med OYV i svaret. Her er slik jeg tenkte.
Siden radiusen i den lille sirkelen er $3$ og radiusen i den store sirkelen er $12$ må $C_1C_2 = 3+12 = 15$.
Hvis en linje $l$ tangerer en sirkel i et punkt $P$ vil linjen fra $P$ til radius i sirkelen stå vinkelrett på linjen $l$. I vårt tilfelle betyr det at $\angle C_1PC_2 = C_1QC_2 = 90^{\circ}$
Både $C_1Q$ og $C_1P$ tangerer sirkelen må de være like lange. Vi har også at $PC_2 = QC_2$ fordi de begge er radius i sirkelen. Derfor må altså $\triangle C_1QC_2 \cong \triangle C_1PC_2$.
Da er arealet gitt ved $\displaystyle A_{C_1PC_2Q} = {2\cdot A_{C_1PC_2}}$
Vi finner $C_1P$ ved Pythagoras:
$(C_1C_2)^2 = (C_1P)^2 + (PC_2)^2$
$(C_1C_2)^2 - (PC_2)^2 = (C_1P)^2$
$C_1P = \sqrt{15^2 - 12^2} = \sqrt{81} = 9$
Da blir altså arealet av firkanten lik: $A_{C_1PC_2Q} = 2 \cdot \frac{9 \cdot 15}{2} = 108$
Re: Geometri og areal
Lagt inn: 04/11-2017 21:17
av Janhaa
Begge er sjølsagt riktige, fine løsninger. Sikkert tiltenkte metoder på oppgava også!
Jeg løste den via et punkts potens (a power of a point):
[tex]CP^2 =3*27=81[/tex]
[tex]CP>0[/tex]
[tex]CP=9[/tex]
så:
[tex]A(C_1PC_2Q) = 9*12=108[/tex]
Re: Geometri og areal
Lagt inn: 05/11-2017 12:09
av Markus
Janhaa skrev:Begge er sjølsagt riktige, fine løsninger. Sikkert tiltenkte metoder på oppgava også!
Jeg løste den via et punkts potens (a power of a point):
[tex]CP^2 =3*27=81[/tex]
[tex]CP>0[/tex]
[tex]CP=9[/tex]
så:
[tex]A(C_1PC_2Q) = 9*12=108[/tex]
Elegant!
