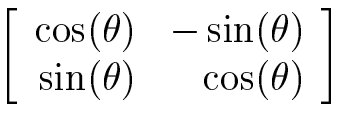Jeg satt så opp standarmatrisa slik:
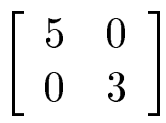
Deretter er neste oppgave å finne standardmatrisa til lineærtransofmrasjonen osm først roterer vektoeren med 45* og deretter strekkresultatet ved U (som jeg fant først).
Her er svaret (fasit) på bare rotasjonen i seg selv:
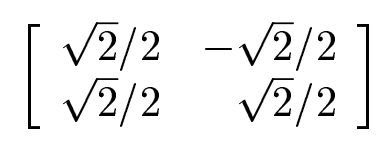
Hvorfor blir det -[tex]-\frac{\sqrt{2}}{2}[/tex] på høyre siden, øverste rad? Hva bestemmer det?
Og hvorfor fungerer ikke det på samme måte som med den første oppgaven hvor jeg skulle finne standarmatrisa?
Der fikk jeg [tex]\frac{5}{0}\frac{0}{3}[/tex] pga. [tex]\frac{1}{0}\frac{0}{1}[/tex]
Fungerer det ikke slik på rotasjon også? F.eks
[tex]\frac{cos}{0}\frac{0}{sin}[/tex]?
Noen som kan forklare dette på en enkel måte, og hvordan man skal tenke? Hvorfor blir det - i denne oppgaven på øverste-høyre rad i rotasjonen? Hvorfor skal man ikke bruke [tex]\frac{1}{0}\frac{0}{1}[/tex] her? Mtp. cos og sin.