Fysikk: Regne ut hvor høyt et prosjektil kommer

[test123476]

I oppgave a er jeg usikker på hvordan jeg skal gå frem. Skal jeg dekomponere slik som dette?



Deretter sette:

[tex]Fx = G \cdot sin(45.6)[/tex]
[tex]Fy = G \cdot cos(45.6)[/tex]

Også eventuelt, [tex]\sum F=ma[/tex] for å finne akselerasjon. Deretter bruke en av bevegelseslikningene?

[Gjest]

Du er litt på villspor, men ikke helt. Du skal bare dekomponere farten i vx og vy uten å bry deg om tyngdekraften. Tyngdekraften virker alltid nedover den så den trenger du ikke å dekomponere. Når du tegner må du sørge for at vx, vy og v skal danne en rettvinklet trekant med v som hypotenus. Altså skal vx være like stor som v strekker seg i horisontal retning og vy skal være like stor som v strekker seg i vertikal retning.

Gjør du dette riktig finner du at vy = v sin(vinkelen) og vx = v cos(vinkelen)
Akselerasjonen trenger du ikke å finne fordi den vet du er den samme som tyngdeakselerasjonen (og virker i negativ retning).
Så kan du bruke en av bevegelsesligningene. Husk at farten i x retning ikke har noe å si for hvor høyt kula kommer (altså hvor langt den går i y retning)

[Kay]

I oppgave a er jeg usikker på hvordan jeg skal gå frem. Skal jeg dekomponere slik som dette?



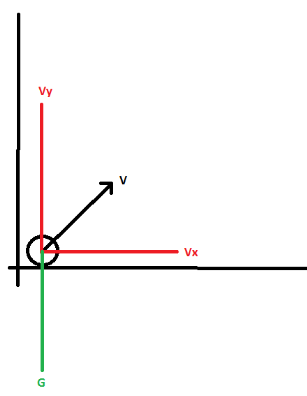
Deretter sette:

[tex]Fx = G \cdot sin(45.6)[/tex]
[tex]Fy = G \cdot cos(45.6)[/tex]

Også eventuelt, [tex]\sum F=ma[/tex] for å finne akselerasjon. Deretter bruke en av bevegelseslikningene?

[tex]v_0= 14\frac{m}{s}[/tex]

Ved trigonometrisk dekomponering av farts-vektoren får vi at

[tex]sin(\alpha)=\frac{v_{0y}}{v_0}\Leftrightarrow v_{0y}= v_0sin(\alpha)[/tex]

[tex]cos(\alpha)=\frac{v_{0x}}{v_0}\Leftrightarrow v_{0x}=v_0cos(\alpha)[/tex]

For å finne høyeste punkt i banen trenger du en eller annen tid.

I det høyeste punktet er [tex]v_y=0[/tex] slik at [tex]v_{0y}+a_yt=0[/tex], så løser du denne og finner en tidsverdi.

Du vet at strekningsvektoren [tex]\vec{s}_y(t)=(v_{0y}t+\frac{1}{2}a_yt^2)[/tex] og nå som du har funnet t setter du bare inn.