|
||||||||||||
 HJEM HJEM |
||||||||||||
| Sannsynlighet | ||||||||||||||||||||||||||||||||
|
Del 1. Mest for ungdomsskolen | Eksperimentell Sannsynlighet | Teoretisk Sannsynlighet | Disjunkte Hendelser | Uavhengige Hendelser | DEL 2. Mest for videregående skole, men bygger på del 1. | Avhengige Hendelser | Kombinatorikk | Ordnet Utvalg med Tilbakelegging | Ordnet Utvalg uten Tilbakelegging | Uordnet Utvalg uten Tilbakelegging | Uordnet Utvalg med Tilbakelegging Hendelser som kan forutsies kalles deterministiske. Hendelser vi ikke kan forutsi, som for eksempel terningkast, kalles tilfeldige forsøk. Hvor mange utfall kan et terningkast ha? En terning har øyner fra en til seks, det betyr at utfallet vil være blant disse. Vi kaller alle mulige utfall for utfallsrommet. Et enkelt utfall vil være et element i utfallsrommet:
U = { 1, 2, 3, 4, 5, 6 }
Hva er sjansen for å få fire øyner? Vi kan angripe problemet på to måter: La oss tenke oss at vi kaster en terning 100 ganger og får 14 firere. Vi sier da at den relative frekvensen for firere etter 100 kast er 14/100 = 0,14 = 14%. Sannsynligheten er lik den relative frekvens i "det lange løp". Dersom vi fortsetter å kaste terningen vil vi oppdage at antall firere vil gå mot et bestemt tall. Vi kan ikke si at sannsynligheten for å få fire er 14% fordi hundre kast er lite i forhold til "det lange løp". La oss prøve en annen mulighet. Utfallsrommet viser oss at det er seks mulige utfall når vi kaster en terning. Vi er bare interessert i å få en firer. Bare en av seks muligheter gir en firer. Det betyr at sannsynligheten for å få en firer i et kast er 1/6 eller 0,167 eller 16,7%. Vi kan skrive det slik:
P (4) = 1/6 = 16,7%
Vi går ut fra at sannsynligheten for å få en treer er like stor som for en firer eller et av de andre utfallene. Når det er slik sier vi at vi har en uniform sannsynlighet. Om våre teoretiske sannsynlighetsmodeller er gode, er det kun utprøving som kan fortelle oss. Når vi har en uniform sannsynlighetsmodell er sannsynligheten for en hendelse gitt ved:
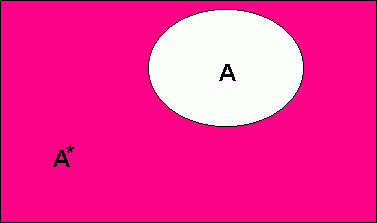
Hva er sannsynligheten for å få en femmer eller en sekser i et terningkast? Sannsynligheten for å få en femmer er 1/6 og sannsynligheten for å få en sekser er 1/6. Sannsynligheten for femmer eller sekser blir da: Hva er så sannsynligheten for å få 1, 2, 3, 4, 5 eller 6? Det blir: Dersom vi kaller sannsynligheten for å få 6 for P(A), vil sannsynligheten for ikke å få 6 være P(A*). Vi har da følgende relasjon:
Hendelser som ikke er A skrives A*. Utfallsrommet kan illustreres slik: Eks: I en klasse er det noen elever som spiller fotball på fritiden. Disse er A. De som ikke spiller fotball er A*. La oss se litt på flere skrivemåter.
Hendelsen A Eks: A er alle i klassen som spiller fotball på fritiden.
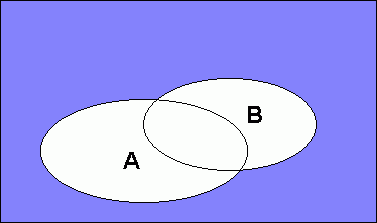
B er alle som driver friidrett. A Hendelsen A Eks: A er alle i klassen som spiller fotball på fritiden.
B er alle som driver friidrett. A Vi har:
Utrykket kalles for addisjonssetningen. Ved å betrakte figuren over ser vi at
leddet -P(A kalles det når det ikke er utfall i A
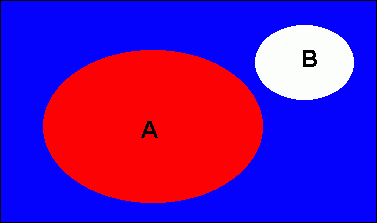
Eks: A er alle i klassen som spiller fotball på fritiden.
B er alle som driver friidrett. Ingen gjør begge deler. Dersom vi benytter (3) på disjunkte hendelser ser vi at det siste leddet forsvinner og addisjonssetningen får følgende form:
Dersom vi kaster en terning en gang, så en gang til, er ikke det andre utfallet påvirket av det første. Slike situasjoner kaller vi for uavhengige hendelser. Hva er sannsynligheten for å få to seksere når vi kaster en terning to ganger? Antall kombinasjoner er som følger: Dersom A (første kast) og B (andre kast) er uavhengige hendelser er:
(produktsetningen for uavhengige hendelser.) Sannsynligheten for å få en sekser i første kast er 1/6. Sannsynligheten er den samme i andre kast. Ved å sette inn i (5) ser vi at sannsynligheten for to seksere er 1/36 og det er i samsvar med vår oppstilling av antall kombinasjoner. Hva er sannsynligheten for å få minst en sekser på to kast? Vi kan da få en sekser i første kast, eller i andre kast, eller vi kan få en sekser i begge kastene. Her er antall mulige kombinasjoner. Av og til kan det være lettere å regne ut antall ugunstige utfall. Hva er sannsynligheten for ikke å få 6 i første kast? Jo, den er 5/6 og det er det samme som for andre kast. Sannsynligheten for ikke å få en sekser i det hele tatt blir da 25/36. Sannsynligheten for minst en sekser må da være 1-25/36 = 11/36. Vi kan se at det stemmer bra med oppstillingen over. DEL 2. Mest for videregående skole, men bygger på del 1. Når vi kaster en terning to ganger er ikke det andre kastet avhengig av resultatet fra første kast. Dersom vi trekker to kort uten tilbakkelegging fra en kortstokk, vil den andre trekningen være avhengig av den første. I en klasse med 30 elever spiller 10 fotball og 5 driver friidrett. 2 gjør begge deler. Vi setter opp et valgtre og får følgende:
Vi finner følgende sannsynligheter: Sannsynligheten for at en tilfeldig elev ikke spiller fotball: P(A*) = 20/30 = 0,6667 Sannsynligheten for at en tilfeldig elev spiller fotball: P(A) = 1 - P(A*) = 0,3333. Du kan også regne denne direkte fra informasjonen du har i utgangspunktet : P(A) = 10/30 = 0,3333. Vi ser at det stemmer bra med valgtreet (selv om det bare har to desimaler i utregningen). Sannsynligheten for at en tilfeldig elev spiller fotball og driver friidrett: P(A
Sannsynligheten for at en tilfeldig elev spiller fotball, men ikke driver friidrett: P(A
Sannsynligheten for at en tilfeldig elev ikke spiller fotball, men driver friidrett: P(A*
Sannsynligheten for at en tilfeldig elev ikke driver med fotball eller friidrett: P(A*
En elev driver friidrett. Hva er sannsynligheten for at eleven spiller fotball? Vi ønsker å finne P(A | B). Vi har: P( fotball og friidrett ) = P (friidrett) · P ( fotball gitt friidrett ) Litt mer matematisk:
Denne setningen kalles produktsetningen for avhengige hendelser, eller den generelle produktsetningen. Dette gir følgende:
Som er den setningen vi bruker på betinget sannsynlighet. Dersom vi setter inn tall i vårt eksempel får vi P(A | B) = 0,0666/0,1666 = 0,4 (P(B) = 0,1 + 0,0666 fordi hendelsene "spiller fotball og driver friidrett" og "spiller ikke fotball men driver friidrett" ikke kan opptre samtidig og derved er disjunkte.) Ved å bruke samme tankegang som over finner vi også:
Dersom vi kombinerer (7) og (8) har vi at:
Setningen kalles Bayes formel. La oss telle litt... På hvor mange måter kan vi arrangere n elementer? n = 1 Muligheter: 1 n = 2 Muligheter: 2·1 = 2 n = 3 Muligheter: 3·2·1 = 6 n = 4 Muligheter: 4·3·2·1 = 24 Dette leder oss til følgende formel:
En n med utropstegn bak leser vi "n fakultet". Det betyr:
n! = n·(n-1)· .. 4·3·2·1
Ordnet Utvalg med Tilbakelegging Nummererte kuler trekkes fra en urne. Rekkefølgen har betydning. Kulen legges tilbake før neste trekning. Ved første trekning kan vi velge mellom n elementer. Siden kulen blir lagt tilbake i urnen før neste trekning er dette situasjonen for k trekninger. Antall muligheter blir:
Eks: Vi trekker 3 nummererte kuler fra en urne med 7 kuler nummerert 1 - 7. Hvor mange muligheter finnes?
73 = 343
Det finnes 343 mulige kombinasjoner Eks: Hva er muligheten for å vinne i fotballtipping? Tenk deg en urne med 3 baller med bokstavene H, U og B. Vi trekker og legger ballen tilbake i urnen. Dette gjentar vi 12 ganger. Antall kombinasjoner på en tippekupong blir da:
312 = 531441
Sannsynligheten for å vinne dersom man tipper en rekke blir da 1:531441, eller litt under to millionedels sjanse. Ordnet Utvalg uten Tilbakelegging Nummererte kuler trekkes fra en urne. Rekkefølgen har betydning. Kulen legges ikke tilbake før neste trekning. Ved første trekning kan vi velge mellom n elementer. Ved andre trekning kan vi velge mellom (n-1) elementer. Antall mulige kombinasjoner:
Hvor vi trekker k elementer fra n elementer. Eks: Vi trekker 3 nummererte kuler fra en urne med 7 kuler nummerert 1 - 7. Hvor mange muligheter finnes? Det finnes 210 forskjellige muligheter. Uordnet Utvalg uten Tilbakelegging Nummererte kuler trekkes fra en urne. Rekkefølgen har ikke betydning. Kulen legges ikke tilbake før neste trekning. Fra ordnet utvalg uten tilbakelegging har vi (12): Vi har sett at k elementer kan arrangeres på k! måter. Siden rekkefølgen her ikke har betydning deler vi formelen over med k! og får:
Utrykket kalles for binominalkeffisienten. Eks: Vi trekker 3 nummererte kuler fra en urne med 7 kuler nummerert 1 - 7. Hvor mange muligheter finnes? Vi benytter () og får: Det finnes 35 muligheter. Eks: I Lotto skal du plukke ut 7 forskjellige tall av 34 mulige (vi ser bort fra tilleggstall). Vi får:
Med 5.379.616 kombinasjoner er det ca. 10 ganger mindre sannsynlig at man treffer hovedgevinsten i Lotto enn i fotballtipping. Uordnet Utvalg med Tilbakelegging Nummererte kuler trekkes fra en urne. Rekkefølgen har ikke betydning. Kulen legges tilbake før neste trekning. Det er lite sannsynlig at du får bruk for dette avsnittet, men det er tatt med for fullstendighetens skyld. Vi har følgende relasjon:
Eks: Vi trekker 3 nummererte kuler fra en urne med 7 kuler nummerert 1 - 7. Hvor mange muligheter finnes? Det er 84 muligheter.
|
||||||||||||||||||||||||||||||||
© 2000- 2024 Sivilingeniør Kenneth Marthinsen, org. no: 976 773 934.
Telefon 932 99 111 Postadr. Odvar Solbergs vei 112, 0973 OSLO
MAIL OSS
|
|
||